题目内容
已知定义在R上的函数y=f(x)满足以下三个条件:
①对于任意的x∈R,都有 f(x+1)=
;
②函数y=f(x+1)的图象关于y轴对称;
③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2).
则f(
),f(2),f(3)从小到大排列是 .
①对于任意的x∈R,都有 f(x+1)=
| 1 |
| f(x) |
②函数y=f(x+1)的图象关于y轴对称;
③对于任意的x1,x2∈[0,1],且x1<x2,都有f(x1)>f(x2).
则f(
| 3 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:对任意的x∈R都有f(x+1)=
得到函数是一个周期函数T=2,根据f(x+1)的图象关于y轴对称,得到f(x)的图象关于x=1对称.对于任意的0≤x1<x2≤1,都有f(x1)>f(x2),得到函数在[0,1]上是一个递减函数,问题得以解决.
| 1 |
| f(x) |
解答:
解:∵f(x+2)=
=f(x),故函数为周期为2的周期函数,
∵f(x+1)的图象关于y轴对称,
∴f(x)的图象关于x=1对称,
∵对于任意的0≤x1<x2≤1,都有f(x1)>f(x2)
∴函数在[0,1]上是一个递减函数,
∴函数在[-1,0]上是一个递增函数,
∵f(
)=f(2-0.5)=f(-0.5),f(2)=f(2+0)=f(0),f(3)=f(4-1)=f(-1)
∴f(3)<f(
)<f(2)
故答案为:f(3)<f(
)<f(2)
| 1 |
| f(x+1) |
∵f(x+1)的图象关于y轴对称,
∴f(x)的图象关于x=1对称,
∵对于任意的0≤x1<x2≤1,都有f(x1)>f(x2)
∴函数在[0,1]上是一个递减函数,
∴函数在[-1,0]上是一个递增函数,
∵f(
| 3 |
| 2 |
∴f(3)<f(
| 3 |
| 2 |
故答案为:f(3)<f(
| 3 |
| 2 |
点评:本题主要考查函数的奇偶性、单调性、周期性,体现了转化的数学思想,属于基础题

练习册系列答案
相关题目
下列结论中是错误命题的是( )
| A、命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0” | ||||
| B、若¬p是q的必要条件,则p是¬q的充分条件 | ||||
C、“M>N”是“(
|
已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=
-a(x≠0)有且仅有3个零点,则a的取值范围是( )
| [x] |
| x |
A、[
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、[
|
函数f(x)=
的图象关于原点对称,g(x)=lg(10x+1)+bx是偶函数,则a+b=( )
| 9x-a |
| 3x |
| A、1 | ||
| B、-1 | ||
C、-
| ||
D、
|
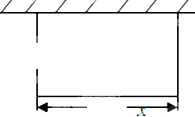 某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为x米,钢筋网的总长度为y米.