题目内容
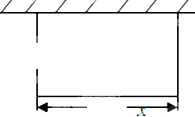某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．（1）列出y与x的函数关系式，并写出其定义域；
（2）问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？
考点：函数模型的选择与应用
专题：应用题,不等式的解法及应用
分析：（1）求出矩形的宽，可得y与x的函数关系式，并写出其定义域；
（2）用到基本不等式的性质注意能否取到“=”．
（2）用到基本不等式的性质注意能否取到“=”．
解答：
解：（1）矩形的宽为：
米，
y=2•
-3+x=
+x-3
定义域为{x|0＜x＜150}
注：定义域为{x|0＜x≤150}不扣分
（2）y=
+x-3≥2
-3=60-3=57
当且仅当
即x=30时取等号，此时宽为：
=15米
所以，长为30米，宽为15米，所用的钢筋网的总长度最小．
| 450 |
| x |
y=2•
| 450 |
| x |
| 900 |
| x |
定义域为{x|0＜x＜150}
注：定义域为{x|0＜x≤150}不扣分
（2）y=
| 900 |
| x |
|
当且仅当
|
| 450 |
| x |
所以，长为30米，宽为15米，所用的钢筋网的总长度最小．
点评：本题主要考查基本不等式的应用，考查运算求解的能力，考查应用意识、函数与方程、化归与转化等数学思想．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=
，则f（f（
））=（ ）
|
| π |
| 4 |
| A、1 | B、-2 | C、2 | D、-1 |
已知f（x-1）=x2，则f（x）的解析式为（ ）
| A、f（x）=x2-2x-1 |
| B、f（x）=x2-2x+1 |
| C、f（x）=x2+2x-1 |
| D、f（x）=x2+2x+1 |
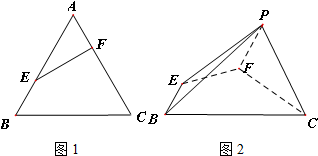在图1等边三角形ABC中，AB=2，E是线段AB上的点（除点A外），过点E作EF⊥AC于点F，将△AEF 沿EF折起到△PEF（点A与点P重合，如图2），使得∠PFC=