题目内容
下列结论中是错误命题的是( )
| A、命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0” | ||||
| B、若¬p是q的必要条件,则p是¬q的充分条件 | ||||
C、“M>N”是“(
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A,写出命题p:“?x∈R,x2-2≥0”的否定形式,再判断正误即可;
B,利用原命题与其逆否命题的等价性可知:¬q是p的必要条件,即p是¬q的充分条件;
C,利用充分必要条件的概念及指数函数的单调性质可判断“M>N”是“(
)M>(
)N”的既不充分又不必要条件.
B,利用原命题与其逆否命题的等价性可知:¬q是p的必要条件,即p是¬q的充分条件;
C,利用充分必要条件的概念及指数函数的单调性质可判断“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:对于A:命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0”,故A正确;
对于B:若¬p是q的必要条件,则¬q是p的必要条件,即p是¬q的充分条件,故B正确
对于C:若M>N,则(
)M<(
)N”,不能得到“(
)M>(
)N”,即充分性不成立;
反之,若“(
)M>(
)N”,则M<N,即必要性也不成立,
∴“M>N”是“(
)M>(
)N”的既不充分又不必要条件,故C错误.
故错误的是:C.
故选:C.
对于B:若¬p是q的必要条件,则¬q是p的必要条件,即p是¬q的充分条件,故B正确
对于C:若M>N,则(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
反之,若“(
| 2 |
| 3 |
| 2 |
| 3 |
∴“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
故错误的是:C.
故选:C.
点评:本题考查命题的真假判断与应用,着重考查命题的否定及等价命题的应用,考查充分必要条件的概念及应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知各项均为正数的等差数列{an}的前20项和为100,那么a2•a19的最大值是( )
| A、50 | ||
| B、25 | ||
| C、100 | ||
D、4
|
已知f(x-1)=x2,则f(x)的解析式为( )
| A、f(x)=x2-2x-1 |
| B、f(x)=x2-2x+1 |
| C、f(x)=x2+2x-1 |
| D、f(x)=x2+2x+1 |
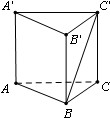 如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为
如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为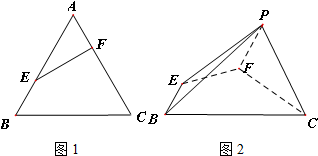 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC= 如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为
如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为