题目内容
已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=
-a(x≠0)有且仅有3个零点,则a的取值范围是( )
| [x] |
| x |
A、[
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、[
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由f(x)=
-a=0,故
=a;分x>0和x<0的情况讨论,显然有a≥0,从而得到答案.
| [x] |
| x |
| [x] |
| x |
解答:
解:因为f(x)=
-a=0,故
=a;
分x>0和x<0的情况讨论,显然有a≥0.
若x>0,此时[x]≥0;
若[x]=0,则
=0;
若[x]≥1,因为[x]≤x<[x]+1,故
<
≤1,即
<a≤1.
且
随着[x]的增大而增大.
若x<0,此时[x]<0;
若-1≤x<0,则
≥1;
若x<-1,因为[x]≤x<-1;[x]≤x<[x]+1,故1≤
<
,即1≤a<
,
且
随着[x]的减小而增大.
又因为[x]一定是不同的x对应不同的a值.
所以为使函数f(x)=
-a有且仅有3个零点,只能使[x]=1,2,3;或[x]=-1,-2,-3.
若[x]=1,有
<a≤1;
若[x]=2,有
<a≤1;
若[x]=3,有
<a≤1;
若[x]=4,有
<a≤1;
若[x]=-1,有a>1;
若[x]=-2,有1≤a<2;
若[x]=-3,有1≤a<
;
若[x]=-4,有1≤a<
综上所述,
<a≤
或
≤a<
,
故选:B.
| [x] |
| x |
| [x] |
| x |
分x>0和x<0的情况讨论,显然有a≥0.
若x>0,此时[x]≥0;
若[x]=0,则
| [x] |
| x |
若[x]≥1,因为[x]≤x<[x]+1,故
| [x] |
| [x]+1 |
| [x] |
| x |
| [x] |
| [x]+1 |
且
| [x] |
| [x]+1 |
若x<0,此时[x]<0;
若-1≤x<0,则
| [x] |
| x |
若x<-1,因为[x]≤x<-1;[x]≤x<[x]+1,故1≤
| [x] |
| x |
| [x] |
| [x]+1 |
| [x] |
| [x]+1 |
且
| [x] |
| [x]+1 |
又因为[x]一定是不同的x对应不同的a值.
所以为使函数f(x)=
| [x] |
| x |
若[x]=1,有
| 1 |
| 2 |
若[x]=2,有
| 2 |
| 3 |
若[x]=3,有
| 3 |
| 4 |
若[x]=4,有
| 4 |
| 5 |
若[x]=-1,有a>1;
若[x]=-2,有1≤a<2;
若[x]=-3,有1≤a<
| 3 |
| 2 |
若[x]=-4,有1≤a<
| 4 |
| 3 |
综上所述,
| 3 |
| 4 |
| 4 |
| 5 |
| 4 |
| 3 |
| 3 |
| 2 |
故选:B.
点评:本题考查了函数的零点问题,考查了分类讨论思想,考查了新定义问题,是一道中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
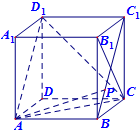 如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:
如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:①AP⊥B1C;
②BP与CD1所成的角是60°;
③VP-AD1C为定值;
④B1P∥平面D1AC;
⑤二面角P-AB-C的平面角为45°.
其中正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知各项均为正数的等差数列{an}的前20项和为100,那么a2•a19的最大值是( )
| A、50 | ||
| B、25 | ||
| C、100 | ||
D、4
|
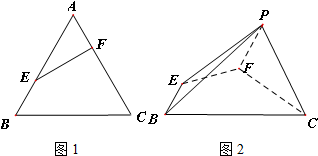 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=