题目内容
函数f(x)=
的图象关于原点对称,g(x)=lg(10x+1)+bx是偶函数,则a+b=( )
| 9x-a |
| 3x |
| A、1 | ||
| B、-1 | ||
C、-
| ||
D、
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由题意可得f(-x)=-f(x)对任意的x都成立,代入整理可求a;由题意可得g(-x)=g(x)对任意的x都成立,代入整理可求b
解答:
解:∵f(x)=
关于原点对称,∴函数f(x)是奇函数,∴f(0)=0,∴a=1
∵g(x)=lg(10x+1)+bx是偶函数,∴g(-x)=g(x)对任意的x都成立,
∴lg(10-x+1)-bx=lg(10x+1)+bx,∴lg(
)=lg(10x+1)+2bx
∴-x=2bx对一切x恒成立,∴b=-
,∴a+b=
故选:D
| 9x-a |
| 3x |
∵g(x)=lg(10x+1)+bx是偶函数,∴g(-x)=g(x)对任意的x都成立,
∴lg(10-x+1)-bx=lg(10x+1)+bx,∴lg(
| 10x+1 |
| 10x |
∴-x=2bx对一切x恒成立,∴b=-
| 1 |
| 2 |
| 1 |
| 2 |
故选:D
点评:本题主要考查了奇偶函数的定义的应用,解题中要善于利用奇函数的性质f(0)=0(0在该函数的定义域内)可以简化基本运算,属于基础题,但是容易出现错误.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
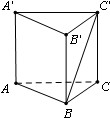 如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为
如图,在三棱柱ABC-A′B′C′中,底面ABC是正三角形,AA′⊥底面ABC,且AB=1,AA′=2,则直线BC′与平面ABB′A′所成角的正弦值为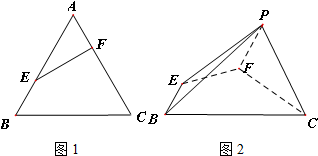 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC= 如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为
如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为