题目内容
在边长为3的正方形ABCD内任取一点P,则P到正方形四边的距离均不小于l的概率为 .
考点:几何概型
专题:概率与统计
分析:本题考查的知识点是几何概型,我们要根据已知条件,求出满足条件的正方形ABCD的面积,及P到正方形四边的距离均不小于1对应平面区域的面积,代入几何概型计算公式,即可求出答案.
解答:
解:满足条件的正方形ABCD,如下图示: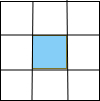
其中满足动点P到正方形四边的距离均不小于1的平面区域如图中阴影所示:
则正方形的面积S正方形=9
阴影部分的面积 S阴影=1
故P到正方形四边的距离均不小于1的概率P=
=
.
故答案为:
.

其中满足动点P到正方形四边的距离均不小于1的平面区域如图中阴影所示:
则正方形的面积S正方形=9
阴影部分的面积 S阴影=1
故P到正方形四边的距离均不小于1的概率P=
| S阴影 |
| S正方形 |
| 1 |
| 9 |
故答案为:
| 1 |
| 9 |
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=
求解.
| N(A) |
| N |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
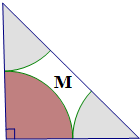 如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域M(图中白色部分).若在此三角形内随机取一点P,则点P落在区域M内的概率为( )
如图,一个等腰直角三角形的直角边长为2,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域M(图中白色部分).若在此三角形内随机取一点P,则点P落在区域M内的概率为( )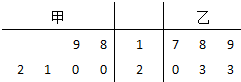 甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示: