Question

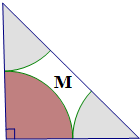如图，一个等腰直角三角形的直角边长为2，分别以三个顶点为圆心，1为半径在三角形内作圆弧，三段圆弧与斜边围成区域M（图中白色部分）．若在此三角形内随机取一点P，则点P落在区域M内的概率为（　　）

• A、

  π

  4

• B、

  π

  2

• C、1-

  π

  4

• D、2-

  π

  2

Answer 1

考点：几何概型

专题：概率与统计

分析：由题意知本题是一个几何概型，先试验发生包含的所有事件是直角三角形的面积S，然后求出阴影部分的面积，代入几何概率的计算公式即可求解

解答： 解：由题意知本题是一个几何概型，
∵试验发生包含的所有事件是直角三角形的面积S=

1

2

×2×2=2，
阴影部分的面积S′=

1

4

π+

π

8

×2=

π

2

，
点P落在区域M内的概率为P=

2- π 2

2

=1-

π

4

．
故选：C．

点评：本题考查几何概型，且把几何概型同几何图形的面积结合起来，几何概型和古典概型是高中必修中学习的，高考时常以选择和填空出现，有时文科会考这种类型的解答．属于基础题．