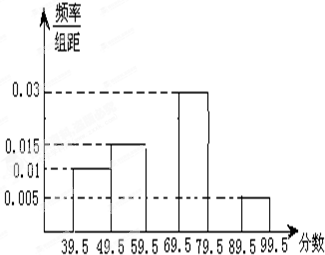
题目内容
已知定义在R上的偶函数f（x）在[0，+∞）上为单调减函数，且f（1-m）＞f（2m），求实数m的取值范围．
考点：奇偶性与单调性的综合
专题：计算题,函数的性质及应用
分析：利用偶函数的性质，f（1-m）＞f（2m），可化为f（|1-m|）＞f（|2m|），由f（x）在区间[0，+∞）上单调递减，得|1-m|＞|2m|，两边平方可解．
解答：
解：∵f（x）是偶函数，∴f（x）=f（|x|），
∴f（1-m）＞f（2m），可化为f（|1-m|）＞f（|2m|），
又f（x）在区间[0，+∞）上单调递减，
∴|1-m|＞|2m|，两边平方，整理得（m+1）（3m-1）＜0，
∴-1＜m＜
．
∴f（1-m）＞f（2m），可化为f（|1-m|）＞f（|2m|），
又f（x）在区间[0，+∞）上单调递减，
∴|1-m|＞|2m|，两边平方，整理得（m+1）（3m-1）＜0，
∴-1＜m＜
| 1 |
| 3 |
点评：本题考查函数的奇偶性、单调性及其综合应用，考查抽象不等式的求解，考查转化思想，属中档题．
练习册系列答案
相关题目
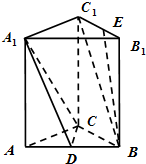如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1，点D是AB的中点，