题目内容
(Ⅰ)解不等式:|3x-1|≤2;
(Ⅱ)设a,b,c∈R+,求证:
+
+
≥
(a+b+c)).
(Ⅱ)设a,b,c∈R+,求证:
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)|3x-1|≤2,等价于-2≤3x-1≤2,由此求得不等式的解集.
(Ⅱ)由于条件利用基本不等式证得
≥
(a+b),同理可得+
≥
(b+c),
≥
(a+c),再利用不等式的性质证得要证的结论.
(Ⅱ)由于条件利用基本不等式证得
| a2+b2 |
| ||
| 2 |
| b2+c2 |
| ||
| 2 |
| c2+a2 |
| ||
| 2 |
解答:
解:(Ⅰ)|3x-1|≤2,等价于-2≤3x-1≤2,等价于-1≤3x≤3,
求得-
≤x≤1,可得不等式的解集为:{x|-
≤x≤1 }.
(Ⅱ)证明:由于a,b,c∈R+,a2+b2≥2ab,∴2(a2+b2)≥a2+b2+2ab=(a+b)2,
即:
≥
(a+b).
同理可得+
≥
(b+c),
≥
(a+c),
因此::
+
+
≥
(a+b+c)成立.
求得-
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)证明:由于a,b,c∈R+,a2+b2≥2ab,∴2(a2+b2)≥a2+b2+2ab=(a+b)2,
即:
| a2+b2 |
| ||
| 2 |
同理可得+
| b2+c2 |
| ||
| 2 |
| c2+a2 |
| ||
| 2 |
因此::
| a2+b2 |
| b2+c2 |
| c2+a2 |
| 2 |
点评:本题主要考查绝对值不等式的解法,基本不等式的应用,属于基础题.

练习册系列答案
相关题目
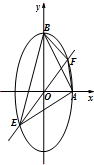 已知椭圆C:
已知椭圆C: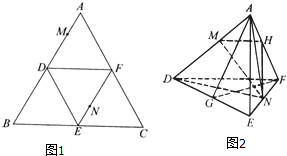 如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.
如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2. 如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.
如图,甲、乙两塔相距120m,在甲塔点A测得乙塔顶的仰角为α,在乙塔点C测得甲塔塔顶的仰角为2α,在两塔间正中一点M测得两塔塔顶的仰角互余,求甲、乙两塔的高度.