题目内容
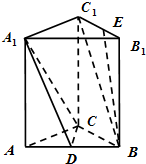如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=BB1，点D是AB的中点，（1）求证：BC1∥平面DCA1；
（2）设点E在线段B1C1上，B1E=λ•B1C1，且使直线BE和平面ABB1A1所成的角的正弦值为
| ||
| 10 |
考点：直线与平面平行的判定,直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：（1）先证明出BC1∥DE，继而根据线面平行的判定定理证明出BC1∥平面CA1D．
（2）过C1，E分别作C1D1⊥A1B1于点D1，EE1⊥A1B1于点E1，连接BE，BE1，可得：∠EBE1即为直线BE和平面ABB1A1所成的角，结合直线BE和平面ABB1A1所成的角的正弦值为
，可得λ的值．
（2）过C1，E分别作C1D1⊥A1B1于点D1，EE1⊥A1B1于点E1，连接BE，BE1，可得：∠EBE1即为直线BE和平面ABB1A1所成的角，结合直线BE和平面ABB1A1所成的角的正弦值为
| ||
| 10 |
解答：
证明：（1）在三棱柱ABC-A1B1C1中，
连接AC1交A1C于点M，连接DM，则M是AC1的中点，
在△ABC1中，点D是AB的中点，所以DM∥BC1，
又DM?平面DCA1，BC1?平面DCA1，
所以BC1∥平面DCA1．
解：（2）在△ABC中，AC⊥BC，AC=BC，点D是AB的中点
所以CD⊥AB，又CD⊥DA1，AB，DA1是平面ABB1A1内的相交直线，
所以CD⊥平面ABB1A1，可知CD⊥BB1．（7分）
又AB⊥BB1，AB∩CD=D，AB，CD?平面ABC，
∴BB1⊥平面ABC，
又∵平面ABC∥平面A1B1C1，
∴BB1⊥平面A1B1C1，
在直三棱柱ABC-A1B1C1中，D是AB的中点，
过C1，E分别作C1D1⊥A1B1于点D1，EE1⊥A1B1于点E1，
连接BE，BE1，
由BB1⊥平面A1B1C1，EE1?平面A1B1C1，
∴BB1⊥EE1，又由EE1⊥A1B1，BB1∩A1B1=B1，BB1，A1B1?平面A1B1BA，
∴EE1⊥平面A1B1BA，
∴BE1即为BE在平面SAB内的射影，
∴∠EBE1即为直线BE和平面ABB1A1所成的角，
设AC=BC=BB1=1，
由B1E=λ•B1C1可得：B1E=λ，
可得：EE1=
λ，BE=
所以在Rt△BE1E中，sin∠EBE1=
=
=
，
解得λ=
（12分）
连接AC1交A1C于点M，连接DM，则M是AC1的中点，
在△ABC1中，点D是AB的中点，所以DM∥BC1，
又DM?平面DCA1，BC1?平面DCA1，
所以BC1∥平面DCA1．
解：（2）在△ABC中，AC⊥BC，AC=BC，点D是AB的中点
所以CD⊥AB，又CD⊥DA1，AB，DA1是平面ABB1A1内的相交直线，
所以CD⊥平面ABB1A1，可知CD⊥BB1．（7分）
又AB⊥BB1，AB∩CD=D，AB，CD?平面ABC，
∴BB1⊥平面ABC，
又∵平面ABC∥平面A1B1C1，
∴BB1⊥平面A1B1C1，
在直三棱柱ABC-A1B1C1中，D是AB的中点，
过C1，E分别作C1D1⊥A1B1于点D1，EE1⊥A1B1于点E1，
连接BE，BE1，
由BB1⊥平面A1B1C1，EE1?平面A1B1C1，
∴BB1⊥EE1，又由EE1⊥A1B1，BB1∩A1B1=B1，BB1，A1B1?平面A1B1BA，
∴EE1⊥平面A1B1BA，
∴BE1即为BE在平面SAB内的射影，
∴∠EBE1即为直线BE和平面ABB1A1所成的角，
设AC=BC=BB1=1，
由B1E=λ•B1C1可得：B1E=λ，
可得：EE1=
| ||
| 2 |
| 1+λ2 |
所以在Rt△BE1E中，sin∠EBE1=
| EE |
| BE |
| ||||
|
| ||
| 10 |
解得λ=
| 1 |
| 2 |
点评：本题考查的知识点是直线与平面垂直的判断，面面垂直的性质，二面的平面角及求法，是空间线面关系和线面夹角的综合应用，难度中档．
练习册系列答案
相关题目
设向量
、
分别对应复数z1、z2，若
⊥
，则
是（ ）
| OZ1 |
| OZ2 |
| OZ1 |
| OZ2 |
| z2 |
| z1 |
| A、非负数 | B、纯虚数 |
| C、正实数 | D、不确定 |