题目内容
已知函数f(x)=4cos2x+4
sinxcosx-1,x∈R.
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且c=2a,求f(B-
)的值.
| 3 |
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且c=2a,求f(B-
| π |
| 12 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)利用倍角公式、两角和差的正弦公式、正弦函数的性质即可得出;
(2)利用等比数列、余弦定理、同角三角函数基本关系式即可得出.
(2)利用等比数列、余弦定理、同角三角函数基本关系式即可得出.
解答:
解:(1)函数f(x)=4cos2x+4
sinxcosx-1=2cos2x+2
sin2x+1=4sin(2x+
)+1,
∴函数f(x) 的最小正周期T=
=π,
∵sin(2x+
)≤1,∴f(x)≤4+1=5,
因此函数f(x)的最大值为5,对应的自变量x的取值集合为{x|x=kπ+
,k∈Z}.
(2)∵在△ABC中,a,b,c成等比数列,∴b2=ac.又c=2a.
∴cosB=
=
=
.∴sinB=
.
∴f(B-
)=4sin2B+1=8sinBcosB+1=
.
| 3 |
| 3 |
| π |
| 6 |
∴函数f(x) 的最小正周期T=
| 2π |
| 2 |
∵sin(2x+
| π |
| 6 |
因此函数f(x)的最大值为5,对应的自变量x的取值集合为{x|x=kπ+
| π |
| 6 |
(2)∵在△ABC中,a,b,c成等比数列,∴b2=ac.又c=2a.
∴cosB=
| a2+c2-b2 |
| 2ac |
| a2+4a2-ac |
| 2a×2a |
| 3 |
| 4 |
| ||
| 4 |
∴f(B-
| π |
| 12 |
3
| ||
| 4 |
点评:本题考查了倍角公式、两角和差的正弦公式、正弦函数的性质、等比数列、余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
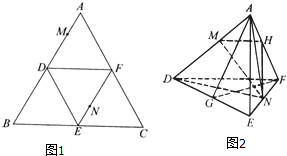 如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.
如图1,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A-DEF如图2.