题目内容
已知函数f(x)=3x3-ax2+x-5在区间[1,2]上单调递减,则a的取值范围是( )
A、[5,
| ||
B、(-∞,5)∪(
| ||
| C、[5,+∞) | ||
D、[
|
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出导函数,欲使函数f(x)在区间[1,2]上单调递减可转化成f′(x)≤0在区间[1,2]上恒成立,再借助参数分离法求出参数a的范围.
解答:
解:f′(x)=9x2-2ax+1
∵f(x)=3x3-ax2+x-5在区间[1,2]上单调递减,
∴f′(x)=9x2-2ax+1≤0在区间[1,2]上恒成立.
即a≥
=
(9x+
),
令g(x)=9x+
,
∴g(x)在[1,2]递增,
∴在[1,2]上,g(x)max=g(2)=
,
∴a≥
×
=
,
故选:D.
∵f(x)=3x3-ax2+x-5在区间[1,2]上单调递减,
∴f′(x)=9x2-2ax+1≤0在区间[1,2]上恒成立.
即a≥
| 9x2+1 |
| 2x |
| 1 |
| 2 |
| 1 |
| x |
令g(x)=9x+
| 1 |
| x |
∴g(x)在[1,2]递增,
∴在[1,2]上,g(x)max=g(2)=
| 37 |
| 2 |
∴a≥
| 1 |
| 2 |
| 37 |
| 2 |
| 37 |
| 4 |
故选:D.
点评:本题主要考查了利用导数研究函数的单调性,以及恒成立问题的转化,属于基础题

练习册系列答案
相关题目
设b>a>0,则2b+
的最小值为 ( )
| 2 |
| ab-a2 |
| A、2 | B、3 | C、6 | D、无最小值 |
函数f(x)=(
)x-4的零点为( )
| 1 |
| 2 |
| A、-2 | B、-1 | C、0 | D、2 |
实验女排和育才女排两队进行比赛,在一局比赛中实验女排获胜的概率是
,没有平局.若采用三局两胜制,即先胜两局者获胜且比赛结束,则实验女排获胜的概率等于( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
使不等式sinx≥
(x∈R)成立的x的集合是( )
| ||
| 2 |
A、{x|x≥
| ||||
B、{x|2kπ+
| ||||
C、{x|
| ||||
D、{x|x≥2kπ+
|
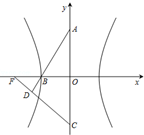 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a>0,b>0,则p=
+
与q=a+b的大小关系为( )
| b2 |
| a |
| a2 |
| b |
| A、p>q | B、p≥q |
| C、p<q | D、p≤q |