题目内容
由两曲线y=sinx(x∈[0,2π])和y=cosx(x∈[0,2π])所围成的封闭图形的面积为 .
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:求出图象的交点坐标,根据定积分的几何意义,所求面积为S=
(cosx-sinx)dx+
(sinx-cosx)dx+
(cosx-sinx)dx,再用定积分计算公式加以运算即可得到本题答案.
| ∫ |
0 |
| ∫ |
|
| ∫ | 2π
|
解答:
解:由y=sinx(x∈[0,2π])和y=cosx(x∈[0,2π]),可得交点坐标为(
,
),(
,
),
∴由两曲线y=sinx(x∈[0,2π])和y=cosx(x∈[0,2π])所围成的封闭图形的面积为
S=
(cosx-sinx)dx+
(sinx-cosx)dx+
(cosx-sinx)dx
=(sinx+cosx)
-(sinx+cosx)
+(sinx+cosx)
=2
.
故答案为:2
.
| π |
| 4 |
| ||
| 2 |
| 5π |
| 4 |
| ||
| 2 |
∴由两曲线y=sinx(x∈[0,2π])和y=cosx(x∈[0,2π])所围成的封闭图形的面积为
S=
| ∫ |
0 |
| ∫ |
|
| ∫ | 2π
|
=(sinx+cosx)
| | |
0 |
| | |
|
| | | 2π
|
| 2 |
故答案为:2
| 2 |
点评:本题求曲线围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设b>a>0,则2b+
的最小值为 ( )
| 2 |
| ab-a2 |
| A、2 | B、3 | C、6 | D、无最小值 |
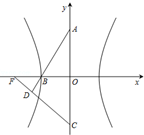 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为3,则∠BDF的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为
已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为直角三角形,则它的体积为