题目内容
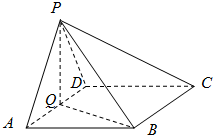 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=2MC,求三棱锥P-QBM的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ))由PA=PD,得到PQ⊥AD,又底面ABCD为菱形,∠BAD=60°,得BQ⊥AD,利用线面垂直的判定定理得到AD⊥平面PQB利用面面垂直的判定定理得到平面PQB⊥平面PAD;
(Ⅱ)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC?平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出.
(Ⅱ)由平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD,得PQ⊥平面ABCD,BC?平面ABCD,得PQ⊥BC,得BC⊥平面PQB,即得到高,利用椎体体积公式求出.
解答:
 (I)证明:∵PA=PD,Q为AD的中点,∴PQ⊥AD,
(I)证明:∵PA=PD,Q为AD的中点,∴PQ⊥AD,
又∵底面ABCD为菱形,∠BAD=60°,∴BQ⊥AD,
又PQ∩BQ=Q,∴AD⊥平面PQB,
又∵AD?平面PAD,∴平面PQB⊥平面PAD;----------------(6分)
(II)解:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD∴PQ⊥平面ABCD,BC?平面ABCD,
∴PQ⊥BC,
又BC⊥BQ,QB∩QP=Q,∴BC⊥平面PQB,
又PM=2MC,∴VP-QBM=VM-PQB=
•
•
•
•
•2=
---------------------------(12分)
 (I)证明:∵PA=PD,Q为AD的中点,∴PQ⊥AD,
(I)证明:∵PA=PD,Q为AD的中点,∴PQ⊥AD,又∵底面ABCD为菱形,∠BAD=60°,∴BQ⊥AD,
又PQ∩BQ=Q,∴AD⊥平面PQB,
又∵AD?平面PAD,∴平面PQB⊥平面PAD;----------------(6分)
(II)解:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD∴PQ⊥平面ABCD,BC?平面ABCD,
∴PQ⊥BC,
又BC⊥BQ,QB∩QP=Q,∴BC⊥平面PQB,
又PM=2MC,∴VP-QBM=VM-PQB=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题给出特殊四棱锥,求证面面垂直并求锥体体积,着重考查了平面与平面垂直的判定、平面与平面垂直的性质和体积公式等知识,属于中档题.

练习册系列答案
相关题目
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点. 如图,已知正四棱锥S-ABCD的底面边长为2,高为
如图,已知正四棱锥S-ABCD的底面边长为2,高为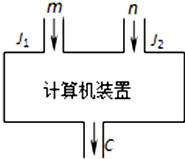 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质: