题目内容
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
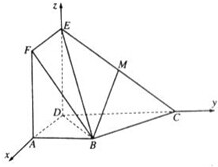
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)当M为CE中点时,求直线BM与平面BEF所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)由已知中矩形ADEF与梯形ABCD所在的平面互相垂直,易得ED⊥平面ABCD,进而ED⊥BC,由勾股定理,我们易判断出△BCD中,BC⊥BD,由线面垂直的判定定理可得BC⊥平面BDE;
(Ⅱ)建立坐标系,求出平面BEF的一个法向量,利用向量的夹角公式,即可求直线BM与平面BEF所成角的正弦值.
(Ⅱ)建立坐标系,求出平面BEF的一个法向量,利用向量的夹角公式,即可求直线BM与平面BEF所成角的正弦值.
解答:
 (Ⅰ)证明:在矩形ADEF中,ED⊥AD,
(Ⅰ)证明:在矩形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
在△BCD中,BD=BC=
,CD=2,
因为BD2+BC2=CD2,所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE;
(Ⅱ)解:建立如图所示的坐标系,则B(1,1,0),E(0,0,1),F(1,0,1),M(0,1,
),
∴
=(0,-1,1),
(1,0,0),
=(-1,0,
),
设
=(x,y,z)为平面BEF的一个法向量,则
,
令y=1得
=(0,1,1).
设直线BM与平面BEF所成角为θ,则
sinθ=|cos<
,
>|=
,
∴直线BM与平面BEF所成角的正弦值为
.
 (Ⅰ)证明:在矩形ADEF中,ED⊥AD,
(Ⅰ)证明:在矩形ADEF中,ED⊥AD,又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
因为BD2+BC2=CD2,所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE;
(Ⅱ)解:建立如图所示的坐标系,则B(1,1,0),E(0,0,1),F(1,0,1),M(0,1,
| 1 |
| 2 |
∴
| BF |
| EF |
| BM |
| 1 |
| 2 |
设
| m |
|
令y=1得
| m |
设直线BM与平面BEF所成角为θ,则
sinθ=|cos<
| m |
| BM |
| ||
| 10 |
∴直线BM与平面BEF所成角的正弦值为
| ||
| 10 |
点评:本题考查的知识点是直线与平面垂直的判定,直线与平面所成角,熟练掌握直线与平面垂直的判定是解答本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
设函数f(x)=sin(ωx+
)(ω>0)与函数g(x)=cos(2x+φ)(|φ|≤
)的对称轴完全相同,则φ的值为( )
| π |
| 4 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知集合A={x|x2-x-6<0},B={x|x2+2x-8>0},则A∩B=( )
| A、{x|-3<x<-2} |
| B、{x|2<x<3} |
| C、{x|-4<x<-2或2<x<3} |
| D、{x|3<x<4} |
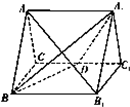 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.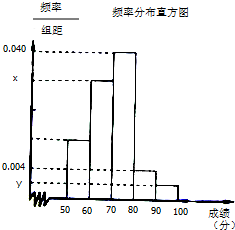 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题: 如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=
如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC= 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若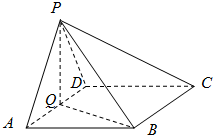 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.