题目内容
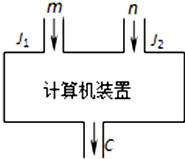 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:①若J1,J2分别输入1,则输出结果为1;
②若J2输入1,J1输入正整数增大1,则输出结果为原的2倍.③若J1输入任何固定正整数不变,J2输入正整数增大1,则输出结果比原减小1;
(1)若J1输入正整数m,J2输入1,则输出结果为多少?
(2)若J1输入正整数m,J2输入正整数n,则输出结果为多少?
(3)若J1与J2依次输入相同的正整数3,4,5,…,n(n≥3),求证:输出结果的倒数和小于1.
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)f (1,1),f (2,1),…,f (m,1),…,组成以f (1,1)为首项,2为公比的等比数列;
(2)f(m,n+1)=f(m,n)-1,所以f(m,1),f(m,2),f(m,3),…,f(m,n),…,组成以f(m,1)为首项,-1为公差的等差数列,由等差数列,等比数列通项公式即可求得.
(3)当n≥3时,f(n,n)>2f(n-1,n-1)>4f(n-2,n-2)>…>2n-3f(3,3)=2n-2,即可证明.
(2)f(m,n+1)=f(m,n)-1,所以f(m,1),f(m,2),f(m,3),…,f(m,n),…,组成以f(m,1)为首项,-1为公差的等差数列,由等差数列,等比数列通项公式即可求得.
(3)当n≥3时,f(n,n)>2f(n-1,n-1)>4f(n-2,n-2)>…>2n-3f(3,3)=2n-2,即可证明.
解答:
解:(1)因为f (m+1,1)=2f (m,1),于是f (1,1),f (2,1),…,f (m,1),…,组成以f (1,1)为首项,2为公比的等比数列,
∴有f (m,1)=f (1,1)?2m-1=2m-1. …3分
(2)因为f(m,n+1)=f(m,n)-1,所以f(m,1),f(m,2),f(m,3),…,f(m,n),…,组成以f(m,1)为首项,-1为公差的等差数列,
∴f(m,n)=f(m,1)-(n-1)=2m-1-(n-1). …7分
(3)由(2)知:f(n,n)=2n-1-(n-1),则f(n+1,n+1)=2n-n,则f(n+1,n+1)-2f(n,n)=n-2>0(n≥3),
∴当n≥3时,f(n,n)>2f(n-1,n-1)>4f(n-2,n-2)>…>2n-3f(3,3)=2n-2,
∴
+
+…+
≤
+
+…
=
<1.…13分.
∴有f (m,1)=f (1,1)?2m-1=2m-1. …3分
(2)因为f(m,n+1)=f(m,n)-1,所以f(m,1),f(m,2),f(m,3),…,f(m,n),…,组成以f(m,1)为首项,-1为公差的等差数列,
∴f(m,n)=f(m,1)-(n-1)=2m-1-(n-1). …7分
(3)由(2)知:f(n,n)=2n-1-(n-1),则f(n+1,n+1)=2n-n,则f(n+1,n+1)-2f(n,n)=n-2>0(n≥3),
∴当n≥3时,f(n,n)>2f(n-1,n-1)>4f(n-2,n-2)>…>2n-3f(3,3)=2n-2,
∴
| 1 |
| f(3,3) |
| 1 |
| f(4,4) |
| 1 |
| f(n,n) |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n-2 |
| ||||
1-
|
点评:本题解题的思想是类比特征,看作是数列问题,利用数列知识求解.

练习册系列答案
相关题目
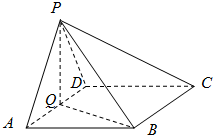 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.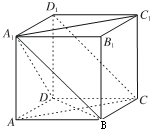 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.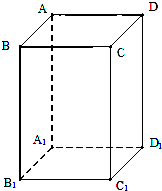 已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求:
已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求: