题目内容
在△ABC中，AB=BC，cosB=-
，若以A，B为焦点的椭圆经过点C．求该椭圆的离心率．
| 7 |
| 18 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：不妨设AB=BC=1，因cosB=-
，则AC2=AB2+BC2-2AB•BC•cosB=
，由此得边AC，再根据椭圆的定义可知2a，又2c=1，从而求出该椭圆的离心率．
| 7 |
| 18 |
| 25 |
| 9 |
解答：
解：设AB=BC=1，则
∵cosB=-
，
∴AC2=AB2+BC2-2AB•BC•cosB=
，
∴AC=
，
∴2a=1+
=
，
∵2c=1，
∴e=
=
．
∵cosB=-
| 7 |
| 18 |
∴AC2=AB2+BC2-2AB•BC•cosB=
| 25 |
| 9 |
∴AC=
| 5 |
| 3 |
∴2a=1+
| 5 |
| 3 |
| 8 |
| 3 |
∵2c=1，
∴e=
| 2c |
| 2a |
| 3 |
| 8 |
点评：本题考查椭圆的性质及应用，解题时要注意的定义的正确运用，属于基础题．
练习册系列答案
相关题目
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形，△ABE中，AB=AE，连结DE，CE，若
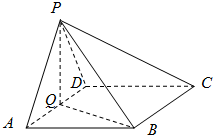如图，在四棱锥中P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
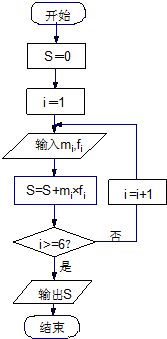“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间（单位：小时），共有2000人参加调查，现将数据整理分组后如题中表格所示．
如图所示，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E．