题目内容
解下列不等式：
（1）-3x2+5x-4＜0
（2）x（1-x）＞x（2x-3）+1．
（1）-3x2+5x-4＜0
（2）x（1-x）＞x（2x-3）+1．
考点：一元二次不等式的解法
专题：计算题,不等式的解法及应用
分析：（1）把不等式整理为标准形式，由△符号及二次函数的图象可得解集；
（2）化简不等式，求出对应方程的根，由图象可得解集；
（2）化简不等式，求出对应方程的根，由图象可得解集；
解答：
解：（1）-3x2+5x-4＜0可化为3x2-5x+4＞0，
△=（-5）2-4×3×4=-23＜0，
则函数y=3x2-5x+4的图象开口向上，与x轴无交点，
∴原不等式的解集为R；
（2）x（1-x）＞x（2x-3）+1可化为3x2-4x+1＜0，即（3x-1）（x-1）＜0，
∴原不等式的解集为{x|
＜x＜1}．
△=（-5）2-4×3×4=-23＜0，
则函数y=3x2-5x+4的图象开口向上，与x轴无交点，
∴原不等式的解集为R；
（2）x（1-x）＞x（2x-3）+1可化为3x2-4x+1＜0，即（3x-1）（x-1）＜0，
∴原不等式的解集为{x|
| 1 |
| 3 |
点评：该题考查一元二次不等式的解法，属基础题，注意数形结合思想在解题中的运用．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
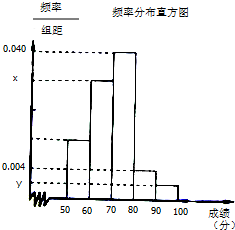某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成的频率分布表和频率分布直方图（如图所示）解决下列问题：
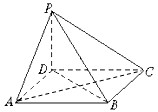如图，四棱锥P-ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD．
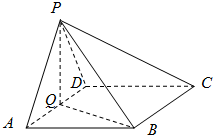如图，在四棱锥中P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
“世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间（单位：小时），共有2000人参加调查，现将数据整理分组后如题中表格所示．
如图所示，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E．