题目内容
已知ω是正实数,函数f(x)=4cosωx•sin(ωx+
)的最小正周期是π.
(Ⅰ)求ω的值;
(Ⅱ)若函数y=f(x)在区间[0,a]内有且仅有2个零点,求正实数a的取值范围.
| π |
| 4 |
(Ⅰ)求ω的值;
(Ⅱ)若函数y=f(x)在区间[0,a]内有且仅有2个零点,求正实数a的取值范围.
考点:二倍角的正弦,两角和与差的正弦函数,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)利用辅助角公式将函数进行化简,利用周期公式即可求ω的值;
(Ⅱ)求出函数函数y=f(x)第2个和第3个零点,结合函数在区间[0,a]内有且仅有2个零点,即可求正实数a的取值范围.
(Ⅱ)求出函数函数y=f(x)第2个和第3个零点,结合函数在区间[0,a]内有且仅有2个零点,即可求正实数a的取值范围.
解答:
解:(Ⅰ)f(x)=4cosωx•sin(ωx+
)=4cosωx•[
(sinωx+cosωx)
=2
sinωxcosωx+2
cos2ωx=
(sin2ωx+1+cos2ωx)=2sin(2ωx+
)+
,
∵函数f(x)的最小正周期是π.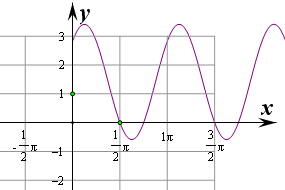
∴T=
=π,即ω=1;
(Ⅱ)当ω=1时,f(x)=2sin(2x+
)+
,
当x=0时,f(0)=2
,
由f(x)=2sin(2x+
)+
=0,
即sin(2x+
)=-
,
当x>0时,2x+
=
,2x+
=
,2x+
=
+2π,…,
则x=
,或x=
,或x=
,
若函数y=f(x)在区间[0,a]内有且仅有2个零点,
则
≤a<
,
求正实数a的取值范围是[
,
).
| π |
| 4 |
| ||
| 2 |
=2
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∵函数f(x)的最小正周期是π.

∴T=
| 2π |
| 2ω |
(Ⅱ)当ω=1时,f(x)=2sin(2x+
| π |
| 4 |
| 2 |
当x=0时,f(0)=2
| 2 |
由f(x)=2sin(2x+
| π |
| 4 |
| 2 |
即sin(2x+
| π |
| 4 |
| ||
| 2 |
当x>0时,2x+
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
则x=
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
若函数y=f(x)在区间[0,a]内有且仅有2个零点,
则
| 3π |
| 4 |
| 3π |
| 2 |
求正实数a的取值范围是[
| 3π |
| 4 |
| 3π |
| 2 |
点评:本题主要考查三角函数的图象和性质,考查学生的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在平面直角坐标系xOy中,已知AB是椭圆
在平面直角坐标系xOy中,已知AB是椭圆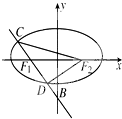 已知椭圆
已知椭圆