题目内容
汽车从刹车开始到完全静止所用的时间叫做刹车时间;所经过的距离叫做刹车距离.某型汽车的刹车距离s(单位米)与时间t(单位秒)的关系为s=5t3-k•t2+t+10,其中k是一个与汽车的速度以及路面状况等情况有关的量.
(1)当k=8时,且刹车时间少于1秒,求汽车刹车距离;
(2)要使汽车的刹车时间不小于1秒钟,且不超过2秒钟,求k的取值范围.
(1)当k=8时,且刹车时间少于1秒,求汽车刹车距离;
(2)要使汽车的刹车时间不小于1秒钟,且不超过2秒钟,求k的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:应用题,导数的综合应用
分析:(1)当k=8时,s=5t3-8t2+t+10,令瞬时速度即s′=0,可求t,再代入s可求;
(2)汽车静止时v=0,故问题转化为15t2-2kt+1=0在[1,2]内有解,2k=
=15t+
,令f(t)=15t+
,利用导数可求得f(t)的范围,从而可得k的范围;
(2)汽车静止时v=0,故问题转化为15t2-2kt+1=0在[1,2]内有解,2k=
| 15t2+1 |
| t |
| 1 |
| t |
| 1 |
| t |
解答:
解:(1)当k=8时,s=5t3-8t2+t+10,
这时汽车的瞬时速度为V=s′=15t2-16t+1,
令s′=0,解得t=1(舍)或t=
,
当t=
时,s=10
,
所以汽车的刹车距离是10
米.
(2)汽车的瞬时速度为v=s′,∴v=15t2-2kt+1,
汽车静止时v=0,
故问题转化为15t2-2kt+1=0在[1,2]内有解,
又2k=
=15t+
,
∵15t+
≥2
,当且仅当15t=
,t=
时取等号,
∵t=
∉[1,2],∴记f(t)=15t+
,f′(t)=15-
,
∵t∈[1,2],∴f′(t)=15-
>0,∴f(t)单调递增,
∴f(t)∈[16,
],2k∈[16,
],即k∈[8,
],
故k的取值范围为k∈[8,
].
这时汽车的瞬时速度为V=s′=15t2-16t+1,
令s′=0,解得t=1(舍)或t=
| 1 |
| 15 |
当t=
| 1 |
| 15 |
| 22 |
| 675 |
所以汽车的刹车距离是10
| 22 |
| 675 |
(2)汽车的瞬时速度为v=s′,∴v=15t2-2kt+1,
汽车静止时v=0,
故问题转化为15t2-2kt+1=0在[1,2]内有解,
又2k=
| 15t2+1 |
| t |
| 1 |
| t |
∵15t+
| 1 |
| t |
| 15 |
| 1 |
| t |
|
∵t=
|
| 1 |
| t |
| 1 |
| t2 |
∵t∈[1,2],∴f′(t)=15-
| 1 |
| t2 |
∴f(t)∈[16,
| 61 |
| 2 |
| 61 |
| 2 |
| 61 |
| 4 |
故k的取值范围为k∈[8,
| 61 |
| 4 |
点评:该题考查导数的几何意义、利用导数求函数的最值,在实际问题中构建恰当函数是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
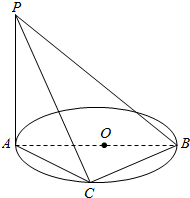 如图,AB是圆O的直径,AB=5,PA垂直于圆O所在的平面,C是圆周上一点,AC=PA=4,求:
如图,AB是圆O的直径,AB=5,PA垂直于圆O所在的平面,C是圆周上一点,AC=PA=4,求: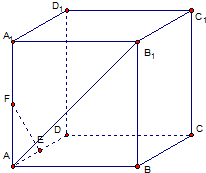 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点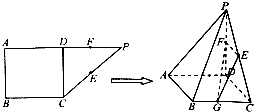 如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=