题目内容
集合S={1，2，3，4，5，6，7，8，9，0}的若干个五元子集满足：S中的任何两个元素至多出现在两个不同的五元子集中，问：至多有多少个五元子集？
考点：排列、组合及简单计数问题
专题：排列组合
分析：因为S中的任何两个元素至多出现在两个不同的五元子集中，
所以两个不同的五元子集中的没有相同的，且元素是全部的集合S的元素，实质就是把10个数平均分成两组，问题得以解决．
所以两个不同的五元子集中的没有相同的，且元素是全部的集合S的元素，实质就是把10个数平均分成两组，问题得以解决．
解答：
解：因为S中的任何两个元素至多出现在两个不同的五元子集中，
所以两个不同的五元子集中的没有相同的，且元素是全部的集合S的元素，实质就是把10个数平均分成两组，
有
=15120．
所以两个不同的五元子集中的没有相同的，且元素是全部的集合S的元素，实质就是把10个数平均分成两组，
有
| ||
| 2 |
点评：本题以集合与元素为数学模型，考查了子集的概念，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
如图，已知ABCD是空间四边形，AB=AD，CB=CD，求证：BD⊥AC．
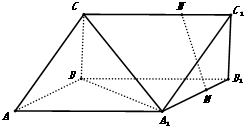如图，三棱柱中ABC-A1B1C1，CA=CB，AB=AA1，∠BAA1=60°，点M和N分别为线段A1B1和CC1上的点，且A1M=2MB1，MN∥平面A1BC．求证：
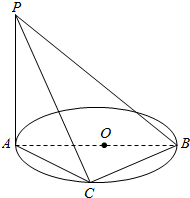如图，AB是圆O的直径，AB=5，PA垂直于圆O所在的平面，C是圆周上一点，AC=PA=4，求：
如图，在△ABC中，AB=AC，过点A的直线与△ABC的外接圆交于点P，交BC的延长线于点D，