题目内容
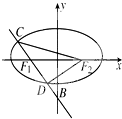 已知椭圆
已知椭圆| x2 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:设直线CD方程为y=-2x-2,由
,得9x2+16x+6=0,由此利用弦长公式和点到直线的距离公式能求出△CDF2的面积.
|
解答:
解:∵椭圆
+y2=1左焦点是F1,∴F1(-1,0)
∴直线CD方程为y=-2x-2,
由
,得9x2+16x+6=0,而△>0,
设C(x1,y1),D(x2,y2),则
,(4分)
∴|CD|=
=
.(8分)
F2到直线DC的距离d=
,
故△CDF2的面积S=
|CD|•d=
.(12分)
| x2 |
| 2 |
∴直线CD方程为y=-2x-2,
由
|
设C(x1,y1),D(x2,y2),则
|
∴|CD|=
(1+4)[(-
|
| 10 |
| 9 |
| 2 |
F2到直线DC的距离d=
4
| ||
| 5 |
故△CDF2的面积S=
| 1 |
| 2 |
| 4 |
| 9 |
| 10 |
点评:本题考查三角形的面积的求法,是中档题,解题时要注意椭圆弦长公式和点到直线的距离公式的灵活运用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
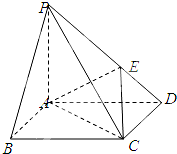 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1. 在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为 在极坐标系中,已知三点O(0,0),A(2,
在极坐标系中,已知三点O(0,0),A(2,