题目内容
在△ABC中,∠BAC=60°,P是△ABC所在平面外一点,PA=PB=PC,∠APB=∠APC=90°.
(1)求证:PB⊥平面PAC;
(2)若H是△ABC的重心,求证:PH⊥平面ABC.
(1)求证:PB⊥平面PAC;
(2)若H是△ABC的重心,求证:PH⊥平面ABC.
考点:直线与平面垂直的判定,直线与平面垂直的性质
专题:
分析:(1)先证明出PB⊥PA,PB⊥PC,根据线面垂直的判定定理证明出PB⊥平面PAC.
(2)作AC的中点D,BC的中点E,连接BD,PD,AE,PE,AE交BD于H,先分别证明出AC⊥面PBD,BC⊥面PAE,进而证明出AC⊥PH,BC⊥PH,最后根据线面垂直的判定定理证明出PH⊥平面ABC.
(2)作AC的中点D,BC的中点E,连接BD,PD,AE,PE,AE交BD于H,先分别证明出AC⊥面PBD,BC⊥面PAE,进而证明出AC⊥PH,BC⊥PH,最后根据线面垂直的判定定理证明出PH⊥平面ABC.
解答:
(1)证明:∵∠APB=∠APC=90°,
∴PB⊥PA,PB⊥PC,
∵PB?平面PAC,PC?平面PAC,PB∩PC=P,
∴PB⊥平面PAC
(2)作AC的中点D,BC的中点E,连接BD,PD,AE,PE,AE交BD于H,
∵PA=PC,
∴PD⊥AC,
∵PB⊥平面PAC,AC?平面PAC,
∴PB⊥AC,
∵PB?平面PBD,PD?平面PBD,PB∩PD=P,
∴AC⊥平面平面PBD,
∴AC⊥PH,
同理可证BC⊥PH,
∵AC?平面ABC,BC?平面ABC,AC∩BC=C,
∴PH⊥平面ABC.
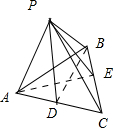
∴PB⊥PA,PB⊥PC,
∵PB?平面PAC,PC?平面PAC,PB∩PC=P,
∴PB⊥平面PAC
(2)作AC的中点D,BC的中点E,连接BD,PD,AE,PE,AE交BD于H,
∵PA=PC,
∴PD⊥AC,
∵PB⊥平面PAC,AC?平面PAC,
∴PB⊥AC,
∵PB?平面PBD,PD?平面PBD,PB∩PD=P,
∴AC⊥平面平面PBD,
∴AC⊥PH,
同理可证BC⊥PH,
∵AC?平面ABC,BC?平面ABC,AC∩BC=C,
∴PH⊥平面ABC.
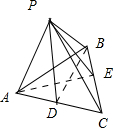
点评:本题主要考查了线面垂直的判定定理的应用.解第二问的最重要的一步是作出H点.

练习册系列答案
相关题目
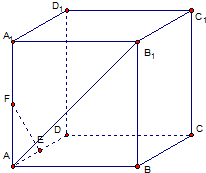 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AD,AA1的中点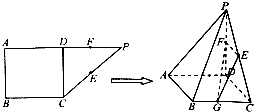 如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC= 如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,
如图,在△ABC中,AB=AC,过点A的直线与△ABC的外接圆交于点P,交BC的延长线于点D,