题目内容
 在平面直角坐标系xOy中,已知AB是椭圆
在平面直角坐标系xOy中,已知AB是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
(1)类比椭圆的上述性质,给出一个在双曲线中也成立的性质;
(2)证明(1)中的结论.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)类比椭圆的性质,直接叙述.
(2)设A(x1,y1),A(x1,y1),M(x0,y0)利用点差法能证明kOM•kAB=
.
(2)设A(x1,y1),A(x1,y1),M(x0,y0)利用点差法能证明kOM•kAB=
| b2 |
| a2 |
解答:
(1)解:在平面直角坐标系xOy中,已知AB是双曲线
-
=1(a>0,b>0)的不平行于对称轴的弦,M为AB的中点,记OM,AB的斜率分别为kOM,kAB,则kOM•kAB=
.…(4分)
(2)证明:设A(x1,y1),A(x1,y1),M(x0,y0)
由
,得:
-
=0,(6分)
∴
-
=0,
∵M(x0,y0)为AB的中点
∴x1+x2=2x0,y1+y2=2y0,(9分)
∴
-
=0,
∴kAB=
=
,(11分)
∵kOM=
,(13分)
∴kOM•kAB=
.(16分)
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
(2)证明:设A(x1,y1),A(x1,y1),M(x0,y0)
由
|
| x12-x22 |
| a2 |
| y12-y22 |
| b2 |
∴
| (x1+x2)(x1-x2) |
| a2 |
| (y1+y2)(y1-y2) |
| b2 |
∵M(x0,y0)为AB的中点
∴x1+x2=2x0,y1+y2=2y0,(9分)
∴
| 2x0(x1-x2) |
| a2 |
| 2y0(y1-y2) |
| b2 |
∴kAB=
| y1-y2 |
| x1-x2 |
| b2 x0 |
| a2y0 |
∵kOM=
| y0 |
| x0 |
∴kOM•kAB=
| b2 |
| a2 |
点评:本题考查双曲线性质的类比叙述,考查两直线的斜率乘积为定值的证明,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
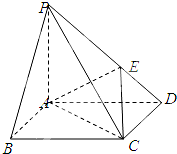 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,点E在PD上,且PE:ED=2:1.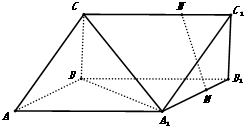 如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证:
如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证: 在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1B1C1D1,且这个几何体的体积为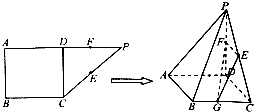 如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=