题目内容
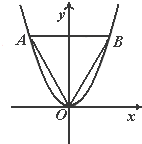 如图,等边三角形OAB的边长为8
如图,等边三角形OAB的边长为8| 3 |
(1)求抛物线C的方程;
(2)设圆M过D(0,2),且圆心M在抛物线C上,EG是圆M在x轴上截得的弦,试探究当M运动时,弦长|EG|是否为定值?为什么?
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知B(4
,12)在抛物线C:x2=2py(p>0)上,由此能求出抛物线C的方程.
(2)设圆的方程为(x-a)2+(y-b)2=a2+(b-2)2,令y=0得:x2-2ax+4b-4=0设圆与x轴的两交点分别为(x1,0),(x2,0),不妨设x1>x2,由此推导出当M运动时,弦长|EG|为定值4.
| 3 |
(2)设圆的方程为(x-a)2+(y-b)2=a2+(b-2)2,令y=0得:x2-2ax+4b-4=0设圆与x轴的两交点分别为(x1,0),(x2,0),不妨设x1>x2,由此推导出当M运动时,弦长|EG|为定值4.
解答:
解:(1)由题意知B(4
,12),
且B在抛物线C:x2=2py(p>0)上,
∴48=24p,解得p=2,
∴抛物线C的方程为x2=4y.
(2)设圆的圆心M(a,b),∵圆M过D(0,2),
∴圆的方程为(x-a)2+(y-b)2=a2+(b-2)2,
令y=0得:x2-2ax+4b-4=0
设圆与x轴的两交点分别为(x1,0),(x2,0)
不妨设x1>x2,
由求根公式得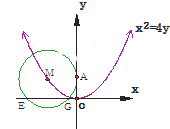 x1=
x1=
,
x2=
…(9分)
∴x1-x2=
又∵点M(a,b)在抛物线x2=4y上,∴a2=4b,…(10分)
∴x1-x2=
=4,即|EG|=4,(13分)
∴当M运动时,弦长|EG|为定值4.
| 3 |
且B在抛物线C:x2=2py(p>0)上,
∴48=24p,解得p=2,
∴抛物线C的方程为x2=4y.
(2)设圆的圆心M(a,b),∵圆M过D(0,2),
∴圆的方程为(x-a)2+(y-b)2=a2+(b-2)2,
令y=0得:x2-2ax+4b-4=0
设圆与x轴的两交点分别为(x1,0),(x2,0)
不妨设x1>x2,
由求根公式得
 x1=
x1=2a+
| ||
| 2 |
x2=
2a-
| ||
| 2 |
∴x1-x2=
| 4a2-16b+16 |
又∵点M(a,b)在抛物线x2=4y上,∴a2=4b,…(10分)
∴x1-x2=
| 16 |
∴当M运动时,弦长|EG|为定值4.
点评:本题考查抛物线方程的求法,探究当M运动时,弦长|EG|是否为定值,解题时要注意函数与方程思想的合理运用.

练习册系列答案
相关题目
已知不共线向量
,
满足|
|=2|
|,且关于x的函数f(x)=-2x3+3|
|x2+6
•
x+5在实数集R上是单调递减函数,则向量
,
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、(0,
| ||
B、(0,
| ||
C、[
| ||
D、[
|
曲线y=
x2-2在x=1处的切线的斜率是( )
| 1 |
| 2 |
| A、0 | ||
| B、1 | ||
| C、-1 | ||
D、
|
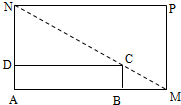 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.