题目内容
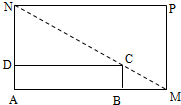如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM上，D在AN上，且对角线MN过C点，已知|AB|=3米，|AD|=2米．（Ⅰ）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？
（Ⅱ）若AN的长不小于4米，试求矩形AMPN的面积的最小值以及取得最小值时AN的长度．
考点：基本不等式在最值问题中的应用,函数最值的应用
专题：函数的性质及应用
分析：（Ⅰ）如图，由题设令AN=x米，然后用x表示出边长|AM|=
，由题意得出
x＞32，从中求出x的范围，即为AN的取值范围．
（Ⅱ）表示出矩形的面积，化简后用基本不等式求出最小值．
| 3x |
| x-2 |
| 3x2 |
| x-2 |
（Ⅱ）表示出矩形的面积，化简后用基本不等式求出最小值．
解答：
解：（Ⅰ）设AN=x米，（x＞2），则ND=x-2
∵
=
，
∴|AM|=
，
∴SAMPN=|AN|•|AM|=
x，
∴
x＞32，
∵x＞2，
∴3x2-32x+64＞0（4分）
∴（3x-8）（x-8）＞0
∴2＜x＜
或x＞8，
即AN长的取值范围是（2，
）∪（8，+∞）；
（Ⅱ）由条件AN的长不小于4，
所以y=
=
=3(x-2)+
+12≥2
+12=24．
当且仅当3(x-2)=
，即x=4时y=
取得最小值，且最小值为24平方米．
答：（Ⅰ）2＜AN＜
或AN＞8
（Ⅱ）当AN的长度是4米时，矩形AMPN的面积最小，最小面积为24平方米．
∵
| |DN| |
| |AN| |
| |DC| |
| |AM| |
∴|AM|=
| 3x |
| x-2 |
∴SAMPN=|AN|•|AM|=
| 3x2 |
| x-2 |
∴
| 3x2 |
| x-2 |
∵x＞2，
∴3x2-32x+64＞0（4分）
∴（3x-8）（x-8）＞0
∴2＜x＜
| 8 |
| 3 |
即AN长的取值范围是（2，
| 8 |
| 3 |
（Ⅱ）由条件AN的长不小于4，
所以y=
| 3x2 |
| x-2 |
| 3(x-2)2+12(x-2)+12 |
| x-2 |
| 12 |
| x-2 |
3(x-2)•
|
当且仅当3(x-2)=
| 12 |
| x-2 |
| 3x2 |
| x-2 |
答：（Ⅰ）2＜AN＜
| 8 |
| 3 |
（Ⅱ）当AN的长度是4米时，矩形AMPN的面积最小，最小面积为24平方米．
点评：本题是个应用题，第一问要求根据题设关系列出函数关系式，并求出处变量的取值范围；第二问考查了基本不等式求最值；本题属于中档题．
练习册系列答案
相关题目
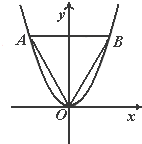如图，等边三角形OAB的边长为8