题目内容
现要对一天的语文,数学,英语,物理,化学,体育共六节课进行排课表.
(1)如果要求物理,化学两门课相邻,共有多少种不同排法?
(2)如果要求语文,数学,英语三门课互不相邻,共有多少种不同排法?
(3)如果要求语文课排在英语课之前,共有多少种不同排法?
(4)如果要求体育课不在第一节,数学课不在第六节,共有多少种不同排法?
(1)如果要求物理,化学两门课相邻,共有多少种不同排法?
(2)如果要求语文,数学,英语三门课互不相邻,共有多少种不同排法?
(3)如果要求语文课排在英语课之前,共有多少种不同排法?
(4)如果要求体育课不在第一节,数学课不在第六节,共有多少种不同排法?
考点:计数原理的应用
专题:排列组合
分析:(1)利用捆绑法,先把物理,化学两门课捆绑在一起看做一个复合元素,再和其它4个元素进行全排,根据分步计数原理可得
(2)利用插空法,先排物理,化学,体育形成4个间隔,再把语文,数学,英语三科插入,根据分步计数原理可得,
(3)利用定序法,全排,因为语文和英语的顺序只有两种,故可求答案.
(4)利用分类法,第一类,数学排在第一节课,第二类,数学不在第一节,根据分类计数原理可得.
(2)利用插空法,先排物理,化学,体育形成4个间隔,再把语文,数学,英语三科插入,根据分步计数原理可得,
(3)利用定序法,全排,因为语文和英语的顺序只有两种,故可求答案.
(4)利用分类法,第一类,数学排在第一节课,第二类,数学不在第一节,根据分类计数原理可得.
解答:
(1)先把物理,化学两门课捆绑在一起看做一个复合元素,再和其它4个元素进行全排,共有
•
=240种不同排法;
(2)先排物理,化学,体育形成4个间隔,再把语文,数学,英语三科插入,共有
•
=144种不同排法;
(3)先全排,因为语文和英语的顺序只有两种,故有
×
=360种不同排法;
(4)分两类,第一类,数学排在第一节课,其它全排,第二类,数学不在第一节,先排第一节,有4种选择,再排第6节有4种选择,最后排其它节次,则有
+4×4
=504种不同排法;
| A | 2 2 |
| A | 5 5 |
(2)先排物理,化学,体育形成4个间隔,再把语文,数学,英语三科插入,共有
| A | 3 3 |
| A | 3 4 |
(3)先全排,因为语文和英语的顺序只有两种,故有
| 1 |
| 2 |
| A | 6 6 |
(4)分两类,第一类,数学排在第一节课,其它全排,第二类,数学不在第一节,先排第一节,有4种选择,再排第6节有4种选择,最后排其它节次,则有
| A | 5 5 |
| ×A | 4 4 |
点评:本题主要考查了排列组合的相邻问题,不相邻问题,顺序问题,特殊元素问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
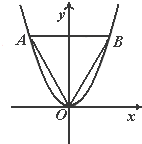 如图,等边三角形OAB的边长为8
如图,等边三角形OAB的边长为8