题目内容
已知函数f(x)=ax3-3x2+1-
,
(1)讨论函数f(x)的单调性;
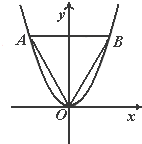
(2)在a>0的情况下,若曲线y=f(x)上两点A,B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
| 3 |
| a |
(1)讨论函数f(x)的单调性;
(2)在a>0的情况下,若曲线y=f(x)上两点A,B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求出函数的导函数,求出相应方程的根,因为二次项的系数为a,要分a>0,和a<0进行讨论.
(2)由曲线y=f(x)上两点A,B处的切线都与y轴垂直,即与x轴平行,A、B为函数的两极值点,又线段AB与x轴有公共点,及两极值应该异号(或其中一个为0).
(2)由曲线y=f(x)上两点A,B处的切线都与y轴垂直,即与x轴平行,A、B为函数的两极值点,又线段AB与x轴有公共点,及两极值应该异号(或其中一个为0).
解答:
解:(1)由a≠0,f′(x)=3ax2-6x=3ax(x-
)
令f'(x)=0得x1=0,x2=
.
(i)当a>0时,
若x∈(-∞,0),则f'(x)>0,所以f(x)在区间(-∞,0)上是增函数;
若x∈(0,
),则f'(x)<0,所以f(x)在区间(0,
)上是减函数;
若x∈(
,+∞),则f'(x)>0,所以f(x)在区间(
,+∞)上是增函数;
(i i)当a<0时,
若x∈(-∞,
),则f'(x)<0,所以f(x)在区间(-∞,
)上是减函数;
若x∈(
,0),则f'(x)>0,所以f(x)在区间(
,0)上是增函数;
若x∈(0,+∞),则f'(x)<0,所以f(x)在区间(0,+∞)上是减函数.
(2)由(1)中(i)的讨论及题设知,
曲线y=f(x)上的两点A,B的纵坐标为函数的极值,且函数y=f(x)在x=0,x=
处分别是取得极大值和极小值
f(0)=1-
,f(
)=-
-
+1.
因为线段AB与x轴有公共点,所以
并且两等号不能同时成立
即
并且两等号不能同时成立,
由已知a>0故
.
解得 3≤a≤4.
即所求实数a的取值范围是[3,4].
| 2 |
| a |
令f'(x)=0得x1=0,x2=
| 2 |
| a |
(i)当a>0时,
若x∈(-∞,0),则f'(x)>0,所以f(x)在区间(-∞,0)上是增函数;
若x∈(0,
| 2 |
| a |
| 2 |
| a |
若x∈(
| 2 |
| a |
| 2 |
| a |
(i i)当a<0时,
若x∈(-∞,
| 2 |
| a |
| 2 |
| a |
若x∈(
| 2 |
| a |
| 2 |
| a |
若x∈(0,+∞),则f'(x)<0,所以f(x)在区间(0,+∞)上是减函数.
(2)由(1)中(i)的讨论及题设知,
曲线y=f(x)上的两点A,B的纵坐标为函数的极值,且函数y=f(x)在x=0,x=
| 2 |
| a |
f(0)=1-
| 3 |
| a |
| 2 |
| a |
| 4 |
| a2 |
| 3 |
| a |
因为线段AB与x轴有公共点,所以
|
即
|
由已知a>0故
|
解得 3≤a≤4.
即所求实数a的取值范围是[3,4].
点评:本题考查了函数的导数,单调性,极值,零点等知识.是一道导数的综合题.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列语句不是命题的是( )
| A、成都外国语学校是一所一流名校. |
| B、如果这道题做不到,那么这次考试成绩不理想. |
| C、?x0∈R,使得lnx0<0. |
| D、滚出去! |
若f(x)=sinx-cosx,则f′(x)等于( )
| A、-cosx-sinx |
| B、cosx-sinx |
| C、sinx+cosx |
| D、-2cosx |
tan70°+tan50°-
tan50°tan70°的值为( )
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图,等边三角形OAB的边长为8
如图,等边三角形OAB的边长为8