题目内容
已知tan(
+α)=3,计算
(1)tanα;
(2)
.
| π |
| 4 |
(1)tanα;
(2)
| sin2x+2cos2x |
| 2cos2x-3sin2x-1 |
考点:二倍角的余弦,两角和与差的正切函数
专题:三角函数的求值
分析:(1)利用两角和的正切公式即可得出;
(2)利用倍角公式、同角三角函数基本关系式即可得出.
(2)利用倍角公式、同角三角函数基本关系式即可得出.
解答:
解:(1)∵tan(
+α)=3,
=3,解得tanα=
.
(2)原式=
=
=
=-
.
| π |
| 4 |
| tanα+1 |
| 1-tanα |
| 1 |
| 2 |
(2)原式=
| 2sinxcosx+2(cos2x-sin2x) |
| 2cos2x-6sinxcosx-sin2x-cos2x |
| 2tanx+2-2tan2x |
| 1-6tanx-tan2x |
2×
| ||||
1-6×
|
| 10 |
| 9 |
点评:本题考查了两角和的正切公式、倍角公式、同角三角函数基本关系式,属于基础题.

练习册系列答案
相关题目
(理科)已知数列{an}的前n项和为Sn,a1=-2,an+1=1-
,则S2013的值为( )
| 1 |
| an |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
tan70°+tan50°-
tan50°tan70°的值为( )
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
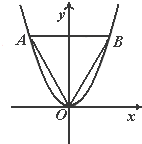 如图,等边三角形OAB的边长为8
如图,等边三角形OAB的边长为8