题目内容
已知变量x，y满足约束条件
，则z=
x+y的最大值为 ．
|
| 1 |
| 2 |
考点：简单线性规划
专题：计算题,作图题,不等式的解法及应用
分析：作出其平面区域，化简z=
x+y为：y=-
x+z，用几何意义解答．
| 1 |
| 2 |
| 1 |
| 2 |
解答：
解：作出其平面区域如下图：
∵z=
x+y的可化为：y=-
x+z，
则过点A（4，3）时，有最大值，
最大值为：5．
故答案为：5．
∵z=
| 1 |
| 2 |
| 1 |
| 2 |
则过点A（4，3）时，有最大值，
最大值为：5．
故答案为：5．
点评：本题考查了简单的线性规划，注意作图要细致，对目标函数化简的方法要注意，属于基础题．
练习册系列答案
相关题目
已知a=（log32）2，b=log322，c=log3（log32），则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、b＞c＞a |
| D、b＞a＞c |
在等比数列{an}中，a1=1，公比|q|≠1．若am=a1a2a3a4a5，则m=（ ）
| A、9 | B、10 | C、11 | D、12 |
在扇形OAB中，∠AOB=120°，P是
上的一个动点，若
=x
+y
，则
+
的最小值是（ ）
 |
| AB |
| OP |
| OA |
| OB |
| 1 |
| x |
| 1 |
| y |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
△ABC中，a=1，b=
，A=30°，则B等于（ ）
| 3 |
| A、60° |
| B、60°或120° |
| C、30°或150° |
| D、120° |
由于被墨水污染，一道数学题仅能见到如下文字：已知二次函数y=x2+bx+c的图象经过（1，0），…，求证：这个二次函数的图象关于直线x=2对称．根据已知信息，题中二次函数图象不具有的性质是（ ）
| A、过点（3，0） |
| B、顶点（2，-2） |
| C、在x轴上截线段长是2 |
| D、与y轴交点是（0，3） |
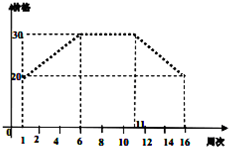在某服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元/件（第一周价格），并且每周价格上涨，如图所示，从第6周开始到第11轴保持30元/件的价格平稳销售；从第12周开始，当季节即将过去时，每周下跌，直到第16周周末，该服装不再销售．