题目内容
在扇形OAB中,∠AOB=120°,P是
上的一个动点,若
=x
+y
,则
+
的最小值是( )
 |
| AB |
| OP |
| OA |
| OB |
| 1 |
| x |
| 1 |
| y |
A、
| ||
| B、2 | ||
C、2
| ||
| D、4 |
考点:基本不等式
专题:平面向量及应用
分析:由P是
上动点,根据
=x
+y
上的一个动点,可知:0≤x≤1,0≤y≤1.因此当x=y=1时,
+
取得最小值.
 |
| AB |
| OP |
| OA |
| OB |
| 1 |
| x |
| 1 |
| y |
解答:
解:如图所示,不妨设A(2,0),则B(-1,
).
由P是
上的一个动点,
=x
+y
=x(2,0)+y (-1,
)=(2x-y,
y).
∵|
|=2,
∴
=2,
化为x2-xy+y2=1.
∴当且仅当x=y=1时
∴
+
的最小值是2.
| 3 |

由P是
 |
| AB |
| OP |
| OA |
| OB |
| 3 |
| 3 |
∵|
| OP |
∴
(2x-y)2+(
|
化为x2-xy+y2=1.
∴当且仅当x=y=1时
∴
| 1 |
| x |
| 1 |
| y |
点评:本题考查了向量共面定理、向量的坐标运算、最小值问题,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在等差数列{an}中,2a3+a9=3,则数列{an}的前9项和等于( )
| A、9 | B、6 | C、3 | D、12 |
已知数列{an}满足a1=
,且对任意的正整数m,n,都有am+n=am•an,则{an}前n项和Sn等于( )
| 2 |
| 3 |
A、2-(
| ||
B、2-(
| ||
C、2-
| ||
D、2-
|
已知集合M={x|log
x<0},N={x|x2≤4},则M∩N=( )
| 1 |
| 2 |
| A、(1,2) |
| B、[1,2) |
| C、(1,2] |
| D、[1,2] |
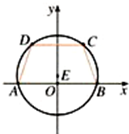 如图,等腰梯形ABCD的底边AB和CD长分别为6和
如图,等腰梯形ABCD的底边AB和CD长分别为6和