题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知
=
.
(Ⅰ)求角A的大小;
(Ⅱ)求4sinB-cosC的取值范围.
| sinA-sinB |
| sinC |
| b+c |
| a+b |
(Ⅰ)求角A的大小;
(Ⅱ)求4sinB-cosC的取值范围.
考点:余弦定理,正弦定理
专题:计算题,解三角形
分析:(Ⅰ)由已知及正弦定理化简可得
=
,即b2+c2-a2b-bc,由余弦定理可得cosA=
=-
,即可求A.
(Ⅱ)化简可得:4sinB-cosC=2sin(2B-
)+
,由0<B<
,可得-
<2sin(2B-
)<
,即可解得4sinB-cosC的取值范围.
| a-b |
| c |
| b+c |
| a+b |
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
(Ⅱ)化简可得:4sinB-cosC=2sin(2B-
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
解答:
(本题满分14分)
解:(Ⅰ)∵
=
,∴
=
…(2分)
即b2+c2-a2b-bc …(4分)
∴cosA=
=-
,
∴A=
…(7分)
(Ⅱ)因为4sinB-cosC=4sinB-cos(
-B)=4sinB(
cosB+
sinB) …(9分)
=2sin2B-
cos2B+
=2sin(2B-
)+
…(11分)
∵0<B<
,∴-
<2B-
<
…(12分)
∴-
<2sin(2B-
)<
,
∴0<4sinB-cosC<2
…(14分)
解:(Ⅰ)∵
| sinA-sinB |
| sinC |
| b+c |
| a+b |
| a-b |
| c |
| b+c |
| a+b |
即b2+c2-a2b-bc …(4分)
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∴A=
| 2π |
| 3 |
(Ⅱ)因为4sinB-cosC=4sinB-cos(
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=2sin2B-
| 3 |
| 3 |
| π |
| 3 |
| 3 |
∵0<B<
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴-
| 3 |
| π |
| 3 |
| 3 |
∴0<4sinB-cosC<2
| 3 |
点评:本题主要考查了三角函数的恒等变换,正弦定理,余弦定理的应用,属于中档题.

练习册系列答案
相关题目
已知不等式组
表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A、B,当∠APB最大时,cos∠APB=( )
|
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
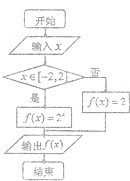 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、(-∞,-2) |
| B、[-2,-1] |
| C、[-1,2] |
| D、(2,+∞) |
某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.为调查产品的销售情况,现进行两种调查:①从这600个销售点中抽取一个容量为100的样本;②在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,则完成①、②这两项调查宜采用的抽样方法依次是( )
| A、分层抽样法,系统抽样法 |
| B、分层抽样法,简单随机抽样法 |
| C、系统抽样法,分层抽样法 |
| D、简单随机抽样法,分层抽样法 |
如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
| A、2:3 | B、2:9 |
| C、4:9 | D、8:27 |
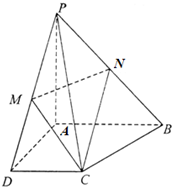 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,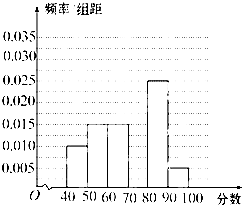 2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: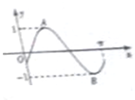 已知函数f(x)=2sinxcos(x-φ)-
已知函数f(x)=2sinxcos(x-φ)-