题目内容
某重点中学今年高中毕业会考成绩的合格率为
，若从参加会考的学生中随机抽取两人，记ξ表示两人成绩不合格的人数，则ξ的方差为 ．
| 37 |
| 40 |
考点：离散型随机变量的期望与方差
专题：概率与统计
分析：由已知得ξ～B（2，
），由此能求出ξ的方差．
| 3 |
| 40 |
解答：
解：由已知得ξ～B（2，
），
∴D（ξ）=2×
×
=
．
故答案为：
．
| 3 |
| 40 |
∴D（ξ）=2×
| 3 |
| 40 |
| 37 |
| 40 |
| 111 |
| 800 |
故答案为：
| 111 |
| 800 |
点评：本题考查离散型随机变量的方差的求法，解题时要认真审题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
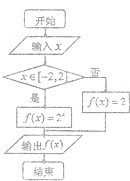阅读如图所示的程序框图，如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、（-∞，-2） |
| B、[-2，-1] |
| C、[-1，2] |
| D、（2，+∞） |
已知函数f（x）=2sinxcos（x-φ）-命题“若x=-1，则x2-x-2=0”的逆否命题是（ ）
| A、若x≠-1，则x2-x-2≠0 |
| B、若x2-x-2≠0，则x≠-1 |
| C、若x=-1，则x2-x-2≠0 |
| D、若x2-x-2≠0，则x=-1 |
在等比数列{an}中，a2a3a7=8，则a4=（ ）
| A、1 | ||
| B、4 | ||
| C、2 | ||
D、2
|
如果两个球的体积之比为8：27，那么两个球的表面积之比为（ ）
| A、2：3 | B、2：9 |
| C、4：9 | D、8：27 |
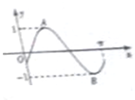
函数f（x）=
的图象大致为（ ）
|
A、 |
B、 |
C、 |
D、 |
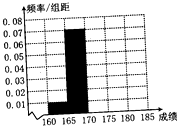某校在自主招生考试成绩中随机抽取100名学生的笔试成绩，被抽取学生的成绩均不低于160分，且低于185分，如图是按成绩分组得到的频率分布图的一部分（每一组均包括左端点数据），且第三组、第四组、第五组的频数之比一次为3：2：1．