题目内容
lg25+lg2•lg50+（lg2）2-（
） -
= ．
| 16 |
| 81 |
| 3 |
| 4 |
考点：对数的运算性质
专题：计算题
分析：根据对数、指数的运算性质将原式化简、求值．
解答：
解：原式=lg25+lg2（lg50+lg2）-[(
)4]-
=lg25+lg2•lg100-(
)-3=lg52+lg2•lg102-
=2（lg5+lg2）-
=2lg10-
=2-
=-
，
故答案为：-
．
| 2 |
| 3 |
| 3 |
| 4 |
=lg25+lg2•lg100-(
| 2 |
| 3 |
| 27 |
| 8 |
=2（lg5+lg2）-
| 27 |
| 8 |
| 27 |
| 8 |
| 27 |
| 8 |
| 11 |
| 8 |
故答案为：-
| 11 |
| 8 |
点评：本题考查对数、指数的运算性质的应用，考查化简、变形能力．
练习册系列答案
相关题目
如果两个球的体积之比为8：27，那么两个球的表面积之比为（ ）
| A、2：3 | B、2：9 |
| C、4：9 | D、8：27 |
若数列{an}满足a1=1，a2=2，anan-2=an-1（n≥3），则a2014的值为（ ）
| A、2 | ||
B、
| ||
| C、1 | ||
| D、22014 |
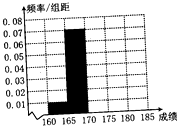某校在自主招生考试成绩中随机抽取100名学生的笔试成绩，被抽取学生的成绩均不低于160分，且低于185分，如图是按成绩分组得到的频率分布图的一部分（每一组均包括左端点数据），且第三组、第四组、第五组的频数之比一次为3：2：1．