题目内容
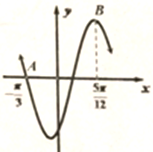 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的最小正周期的公式即可求出ω,由五点法作图可得φ的值.
解答:
解:由图象知
=
-(-
)=
,
即函数的周期T=π,
由T=
=π得ω=2,
∵f(
)=2sin(2×
+φ)=2,
得sin(
+φ)=1,
即
+φ=
+kπ,则φ=kπ-
,k∈Z,
∵-
<φ<
,∴k=0时,φ=-
,
故选:B
| 3T |
| 4 |
| 5π |
| 12 |
| π |
| 3 |
| 3π |
| 4 |
即函数的周期T=π,
由T=
| 2π |
| ω |
∵f(
| 5π |
| 12 |
| 5π |
| 12 |
得sin(
| 5π |
| 6 |
即
| 5π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵-
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
故选:B
点评:本题考查有部分图象确定函数的解析式,本题解题的关键是确定初相的值,这里利用代入点的坐标求出初相.

练习册系列答案
相关题目
命题“若x=-1,则x2-x-2=0”的逆否命题是( )
| A、若x≠-1,则x2-x-2≠0 |
| B、若x2-x-2≠0,则x≠-1 |
| C、若x=-1,则x2-x-2≠0 |
| D、若x2-x-2≠0,则x=-1 |
如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
| A、2:3 | B、2:9 |
| C、4:9 | D、8:27 |
下列四个数中最小者是( )
A、log3
| ||
| B、log32 | ||
| C、log23 | ||
| D、log3(log23) |
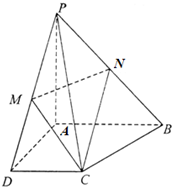 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,