题目内容
已知函数y=（
）n过点P（1，
），求函数在点P处的切线方程．
| x |
| 2x+1 |
| 1 |
| 9 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：把点P（1，
）代入曲线方程求得n的值，求出函数的导函数，得到函数在x=1处的导数，由点斜式得切线方程．
| 1 |
| 9 |
解答：
解：由函数y=（
）n过点P（1，
），
则
=(
)n，得n=2，即y=(
)2，
由y′=
•(
)′=
•
=
，
则在点P处的切线斜率k=y′|x=1=
，
可得切线的方程为y-
=
(x-1)，
即2x-27y+1=0．
| x |
| 2x+1 |
| 1 |
| 9 |
则
| 1 |
| 9 |
| 1 |
| 2+1 |
| x |
| 2x+1 |
由y′=
| 2x |
| 2x+1 |
| x |
| 2x+1 |
| 2x |
| 2x+1 |
| 2x+1-2x |
| (2x+1)2 |
| 2x |
| (2x+1)3 |
则在点P处的切线斜率k=y′|x=1=
| 2 |
| 27 |
可得切线的方程为y-
| 1 |
| 9 |
| 2 |
| 27 |
即2x-27y+1=0．
点评：本题考查了利用导数研究曲线上某点的切线方程，函数在曲线上某点处的导数值，即为曲线在该点处的切线的斜率，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
若不等式
＜1对于一切实数都成立，则k的取值范围是（ ）
| 2x2+2kx+k |
| 4x2+6x+3 |
| A、（-∞，+∞） |
| B、（1，3） |
| C、（-∞，3） |
| D、（-∞，1）∪（3，+∞） |
点P是函数y=x2-2lnx的图象上任意一点，则点P到直线y=3x-1的最小距离是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
掷两颗均匀的大小不同的骰子，记“两颗骰子的点数和为10”为事件A，“小骰子出现的点数大于大骰子出现的点数”为事件B，则P（B|A）为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
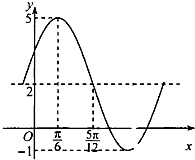已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．
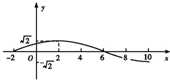已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜