题目内容
计算下列各式:
(1)已知ax=
-
(a>0),求
的值;
(2)0.001-
-(
)0+16
+(
•
)6.
(1)已知ax=
| 6 |
| 5 |
| a3x-a-3x |
| ax-a-x |
(2)0.001-
| 1 |
| 3 |
| 7 |
| 8 |
| 3 |
| 4 |
| 2 |
| 3 | 3 |
考点:根式与分数指数幂的互化及其化简运算
专题:计算题
分析:(1)把要求解得式子的分子展开立方差根式,约分后再配方,代入ax的值化简整理;
(2)化小数为分数,化根式为分数指数幂,然后利用有理指数幂的运算性质求解.
(2)化小数为分数,化根式为分数指数幂,然后利用有理指数幂的运算性质求解.
解答:
解:(1)∵ax=
-
(a>0),
∴
=
=a2x+a-2x+1
=(ax+a-x)2-1
=(
-
+
)2-1
=(
-
+
+
)2-1
=23;
(2)0.001-
-(
)0+16
+(
•
)6
=[(0.1)3]-
-1+(24)
+(2
•3
)6
=10-1+23+23•32
=9+8+72
=89.
| 6 |
| 5 |
∴
| a3x-a-3x |
| ax-a-x |
=
| (ax-a-x)(a2x+1+a-2x) |
| ax-a-x |
=a2x+a-2x+1
=(ax+a-x)2-1
=(
| 6 |
| 5 |
| 1 | ||||
|
=(
| 6 |
| 5 |
| 6 |
| 5 |
=23;
(2)0.001-
| 1 |
| 3 |
| 7 |
| 8 |
| 3 |
| 4 |
| 2 |
| 3 | 3 |
=[(0.1)3]-
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
=10-1+23+23•32
=9+8+72
=89.
点评:本题考查了有理指数幂的运算性质,考查了根式与分数指数幂的互化,是基础的计算题.

练习册系列答案
相关题目
已知随机变量X~B(6,0.4),则当η=-2X+1时,D(η)=( )
| A、-1.88 | B、-2.88 |
| C、5.76 | D、6.76 |
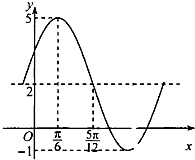 已知函数f(x)=Asin(ωx+φ)+b(A、ω>0,0<φ<π,b为常数)一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A、ω>0,0<φ<π,b为常数)一段图象如图所示.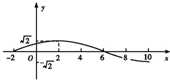 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.