题目内容
已知向量
=(1,2),
=(cosα,sinα),设
=
-t
(t为实数).
(Ⅰ)t=1时,若
∥
,求tanα;
(Ⅱ)若α=
,求|
|的最小值,并求出此时向量
在
方向上的投影.
| a |
| b |
| c |
| a |
| b |
(Ⅰ)t=1时,若
| c |
| b |
(Ⅱ)若α=
| π |
| 4 |
| c |
| a |
| c |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:(I)利用向量共线定理即可得出;
(II)利用数量积的性质可得|
|,再利用二次函数的单调性即可得出其最小值,进而得出投影.
(II)利用数量积的性质可得|
| c |
解答:
解:(I)∵t=1,∴
=(1-cosα,2-sinα),
∵
∥
,
∴cosα(2-sinα)-sinα(1-cosα)=0,
化为2cosα=sinα,
可得tanα=2;
(II)α=
时,|
|=
=
,
当t=
时,|
|min=
,
此时
=(-
,
),
在
方向上的投影
=
.
| c |
∵
| c |
| b |
∴cosα(2-sinα)-sinα(1-cosα)=0,
化为2cosα=sinα,
可得tanα=2;
(II)α=
| π |
| 4 |
| c |
(1-
|
t2-3
|
当t=
3
| ||
| 2 |
| c |
| ||
| 2 |
此时
| c |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| c |
| ||||
|
|
| ||
| 2 |
点评:本题考查了向量共线定理、数量积的性质、二次函数的单调性、投影等基础知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
点P是函数y=x2-2lnx的图象上任意一点,则点P到直线y=3x-1的最小距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
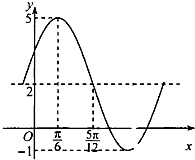 已知函数f(x)=Asin(ωx+φ)+b(A、ω>0,0<φ<π,b为常数)一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A、ω>0,0<φ<π,b为常数)一段图象如图所示.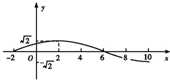 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<