题目内容
已知函数f(x)=ex-1,g(x)=-x2+4x-3,若有f(a)=g(b),则b的取值范围为 .
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:根据函数的单调性求出f(x)的值域,从而得到g(b)的取值范围,解一元二次不等式即可.
解答:
解:∵f(x)=ex-1,在R上是增函数,
∴f(a)>-1,
∴g(b)>-1,
∴-b2+4b-3>-1,
即b2-4b+2<0,
解得2-
<b<2+
;
故答案为:(2-
,2+
).
∴f(a)>-1,
∴g(b)>-1,
∴-b2+4b-3>-1,
即b2-4b+2<0,
解得2-
| 2 |
| 2 |
故答案为:(2-
| 2 |
| 2 |
点评:本题考查了函数的值域以及函数的定义域和一元二次不等式的解法问题,是基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
掷两颗均匀的大小不同的骰子,记“两颗骰子的点数和为10”为事件A,“小骰子出现的点数大于大骰子出现的点数”为事件B,则P(B|A)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=2x-2+3的图象恒过点P,则点P为( )
| A、(2,3) |
| B、(1,1) |
| C、(0,1) |
| D、(2,4) |
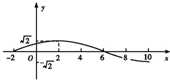 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<