题目内容
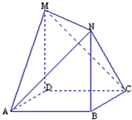 四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.
四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1.(1)以向量
| AB |
(2)求证:CN∥平面AMD;
(3)(理科做,文不做)求面AMN与面NBC所成的锐二面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)由已知条件推导出以向量
方向为侧视方向的侧视图为边长是1的正方形.
(2)以D为原点,DA为x轴,DC为y轴,DM为z轴,建立空间直角坐标系,利用向量法能证明CN∥平面AMD.
(3)分别求出平面NBC的一个法向量和平面AMN的法向量,由此能求出面AMN与面NBC所成的锐二面角的余弦值.
| AB |
(2)以D为原点,DA为x轴,DC为y轴,DM为z轴,建立空间直角坐标系,利用向量法能证明CN∥平面AMD.
(3)分别求出平面NBC的一个法向量和平面AMN的法向量,由此能求出面AMN与面NBC所成的锐二面角的余弦值.
解答:
(1)解:∵四边形ABCD是边长为1的正方形,
MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,
∴AB⊥面BCN,DC⊥面BCN,
∴以向量
方向为侧视方向的侧视图为如图所示的边长是1的正方形.
(2)证明:以D为原点,DA为x轴,DC为y轴,DM为z轴,
建立空间直角坐标系,
由题意知D(0,0,0),A(1,0,0),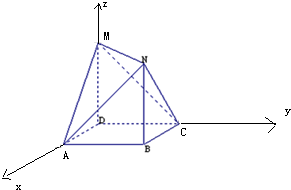 C(0,1,0),
C(0,1,0),
M(0,0,1),N(1,1,1),
∴
=(1,0,1),
∵DC⊥AD,DC⊥DM,AD∩∩DM=D,
∴DC⊥平面AMD,
∴平面AMD的一个法向量为
=(0,1,0),
∵
•
=0,
∴CN∥平面AMD.
(3)解:∵平面NBC∥平面AMD,
∴平面NBC的一个法向量为
=(0,1,0),
设平面AMN的法向量
=(x,y,z),
∵
=(-1,0,1),
=(0,1,1),
∴
,
取x=1,得
=(1,-1,1),
∴cos<
,
>=
=-
.
∴面AMN与面NBC所成的锐二面角的余弦值为
.

MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,
∴AB⊥面BCN,DC⊥面BCN,
∴以向量
| AB |
(2)证明:以D为原点,DA为x轴,DC为y轴,DM为z轴,
建立空间直角坐标系,
由题意知D(0,0,0),A(1,0,0),
 C(0,1,0),
C(0,1,0),M(0,0,1),N(1,1,1),
∴
| CN |
∵DC⊥AD,DC⊥DM,AD∩∩DM=D,
∴DC⊥平面AMD,
∴平面AMD的一个法向量为
| DC |
∵
| DC |
| CN |
∴CN∥平面AMD.
(3)解:∵平面NBC∥平面AMD,
∴平面NBC的一个法向量为
| DC |
设平面AMN的法向量
| n |
∵
| AM |
| AN |
∴
|
取x=1,得
| n |
∴cos<
| n |
| CD |
| -1 | ||
|
| ||
| 3 |
∴面AMN与面NBC所成的锐二面角的余弦值为
| ||
| 3 |
点评:本题考查侧视图的作法,考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
若不等式mx2+mnx+n>0的解集为{x|1<x<2},则m+n的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
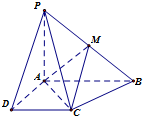 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=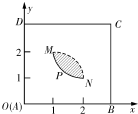 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=