题目内容
证明：x＞0时，ln（x+1）＞
恒成立．
| x |
| x+1 |
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：根据题意可得，要证不等式ln（x+1）＞
恒成立，只需证（x+1）ln（x+1）-x＞0成立，构造函数f（x）=（x+1）ln（x+1）-x，利用导数判断f（x）在x＞0时单调递增，从而得到f（x）＞f（0）=0，即（x+1）ln（x+1）-x＞0成立，即原不等式得证．
| x |
| x+1 |
解答：
解：∵x＞0，
∴要证ln（x+1）＞
，
只需证（x+1）ln（x+1）＞x，
即证（x+1）ln（x+1）-x＞0，
令f（x）=（x+1）ln（x+1）-x，
则f′（x）=ln（x+1）+1-1=ln（x+1），
∵x＞0，
∴ln（x+1）＞ln1=0，
即f′（x）＞0，
∴f（x）在x＞0时单调递增，
∴f（x）＞f（0）=0
∴（x+1）ln（x+1）-x＞0成立，
∴不等式得证．
∴要证ln（x+1）＞
| x |
| x+1 |
只需证（x+1）ln（x+1）＞x，
即证（x+1）ln（x+1）-x＞0，
令f（x）=（x+1）ln（x+1）-x，
则f′（x）=ln（x+1）+1-1=ln（x+1），
∵x＞0，
∴ln（x+1）＞ln1=0，
即f′（x）＞0，
∴f（x）在x＞0时单调递增，
∴f（x）＞f（0）=0
∴（x+1）ln（x+1）-x＞0成立，
∴不等式得证．
点评：本题考查不等式的性质，导数在研究函数单调性中的应用，属于中档题．
练习册系列答案
相关题目
设z=1-i（i是虚数单位），则复数
+i2的实部是（ ）
| 3 |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
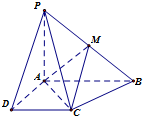已知四棱锥P-ABCD的底面为直角梯形，AB∥CD，∠DAB=
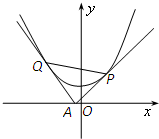过x轴上动点A（a，0），引抛物线y=x2+1的两条切线AP、AQ．切线斜率分别为k1和k2，切点分别为P、Q．
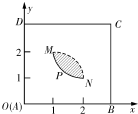如图，矩形ABCD是一个观光区的平面示意图，建立平面直角坐标系，使顶点A在坐标原点O，B，D分别在x轴，y轴上，AD=3百米，AB=a百米（3≤a≤4）观光区中间叶形阴影部分MN是一个人工湖，它的左下方边缘曲线是函数y=