题目内容
已知复数z=（2+i）m2-3m（1+i）-2（1-i），当实数m取什么值时，复数z是
（1）虚数；
（2）纯虚数．
（3）实数．
（1）虚数；
（2）纯虚数．
（3）实数．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：根据复数的有关概念建立条件关系即可得到结论．
解答：
解：z=（2+i）m2-3m（1+i）-2（1-i）=2m2-3m-2+（m2-3m+2）i，
（1）若复数z是虚数，则由m2-3m+2≠0，得m≠1且m≠2．
（2）若复数z是纯虚数，则由
，得m=-
．
（3）若复数z是实数，则m2-3m+2=0，得m=2或m=1．
（1）若复数z是虚数，则由m2-3m+2≠0，得m≠1且m≠2．
（2）若复数z是纯虚数，则由
|
| 1 |
| 2 |
（3）若复数z是实数，则m2-3m+2=0，得m=2或m=1．
点评：本题主要考查复数的有关概念，利用复数的运算法则是解决本题的关键，比较基础．
练习册系列答案
相关题目
设z=2x+5y，其中实数x，y满足6≤x+y≤8且-2≤x-y≤0，则z的最大值是（ ）
| A、21 | B、24 | C、28 | D、31 |
若不等式mx2+mnx+n＞0的解集为{x|1＜x＜2}，则m+n的值为（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设z=1-i（i是虚数单位），则复数
+i2的实部是（ ）
| 3 |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知f1（x）=sinx+cosx，fn+1（x）是fn（x）的导函数，即f2（x）=f1′（x），f3（x）=f2′（x），…，fn+1（x）=fn′（x），n∈N*，则f2014（x）等于（ ）
| A、-sinx-cosx |
| B、sinx-cosx |
| C、sinx+cosx |
| D、-sinx+cosx |
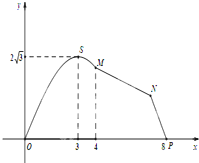如图，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asin（ωx）（A＞0，ω＞0），x∈[0，4]的图象，且图象的最高点为S（3，2
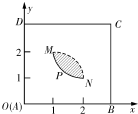如图，矩形ABCD是一个观光区的平面示意图，建立平面直角坐标系，使顶点A在坐标原点O，B，D分别在x轴，y轴上，AD=3百米，AB=a百米（3≤a≤4）观光区中间叶形阴影部分MN是一个人工湖，它的左下方边缘曲线是函数y=