题目内容
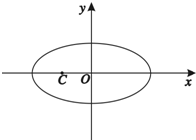 在平面直角坐标系xOy中,椭圆Γ:
在平面直角坐标系xOy中,椭圆Γ:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆Γ的方程;
(Ⅱ)设斜率为k的直线l过点C(-1,0)且交椭圆Γ于A,B两点,试探究椭圆Γ上是否存在点P,使得四边形OAPB为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)椭圆Γ:
+
=1(a>b>0)过点(2,0),焦距为2
,求出a,c,可求b,即可求椭圆Γ的方程;
(Ⅱ)直线y=k(x+1)代入椭圆方程,利用韦达定理,结合椭圆Γ上存在点P(x0,y0)使得四边形OAPB为平行四边形,求出P的坐标,代入椭圆方程,即可得出结论.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅱ)直线y=k(x+1)代入椭圆方程,利用韦达定理,结合椭圆Γ上存在点P(x0,y0)使得四边形OAPB为平行四边形,求出P的坐标,代入椭圆方程,即可得出结论.
解答:
解:(Ⅰ)由已知得a=2,c=
,…(2分)
因为a2=b2+c2,所以b2=a2-c2=1,…(3分)
所以椭圆Γ的方程为
+y2=1;…(4分)
(Ⅱ)依题意得:直线y=k(x+1),设A(x1,y1),B(x2,y2),
假设椭圆Γ上存在点P(x0,y0)使得四边形OAPB为平行四边形,则
.
由
得(1+4k2)x2+8k2x+4(k2-1)=0,…(6分)
所以x1+x2=
,y1+y2=k(x1+x2+2)=k(
+2)=
.…(8分)
于是
即点P的坐标为(
,
). …(10分)
又点P在椭圆上,所以
+(
)2=1,整理得4k2+1=0,此方程无解.…(11分)
故椭圆Γ上不存在点P,使四边形OAPB为平行四边形. …(12分)
| 3 |
因为a2=b2+c2,所以b2=a2-c2=1,…(3分)
所以椭圆Γ的方程为
| x2 |
| 4 |
(Ⅱ)依题意得:直线y=k(x+1),设A(x1,y1),B(x2,y2),
假设椭圆Γ上存在点P(x0,y0)使得四边形OAPB为平行四边形,则
|
由
|
所以x1+x2=
| -8k2 |
| 1+4k2 |
| -8k2 |
| 1+4k2 |
| 2k |
| 1+4k2 |
于是
|
| -8k2 |
| 1+4k2 |
| 2k |
| 1+4k2 |
又点P在椭圆上,所以
(
| ||
| 4 |
| 2k |
| 1+4k2 |
故椭圆Γ上不存在点P,使四边形OAPB为平行四边形. …(12分)
点评:本小题主要考查椭圆的标准方程、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.

练习册系列答案
相关题目
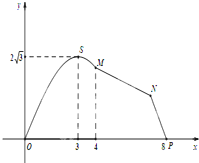 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin(ωx)(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2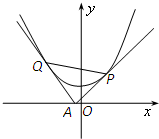 过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.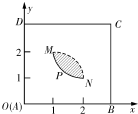 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=