题目内容
已知f(α)=
.
(1)化简f(α);
(2)若f(α)=
,且
<α<
,求cosα-sinα的值.
| sin(π-α)•cos(2π-α)•tan(-π+α) |
| sin(-π+α)•tan(-α+3π) |
(1)化简f(α);
(2)若f(α)=
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)f(α)分子分母利用诱导公式化简,再利用同角三角函数间基本关系化简,计算即可得到结果;
(2)由f(α)=
,求出cosα的值,根据α的范围求出sinα的值,代入原式计算即可求出值.
(2)由f(α)=
| 1 |
| 8 |
解答:
解:(1)f(α)=
=cosα;
(2)∵f(α)=cosα=
,
<α<
,
∴sinα=
=
,
则原式=
-
=
.
| sinαcosαtanα |
| -sinα(-tanα) |
(2)∵f(α)=cosα=
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴sinα=
| 1-cos2α |
3
| ||
| 8 |
则原式=
| 1 |
| 8 |
3
| ||
| 8 |
1-3
| ||
| 8 |
点评:此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系及诱导公式是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
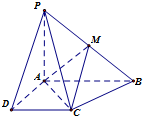 已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=
已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=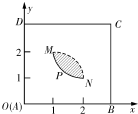 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=