题目内容
定义:min{a,b}=
,在区域
内任取一点P(x,y),则x、y满足min{x2+x+2y,x+y+4}=x2+x+2y的概率为 .
|
|
考点:几何概型
专题:计算题,概率与统计
分析:本题是一个几何概型,试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},算出两个集合对应的面积,面积之比就是要求的概率.
解答:
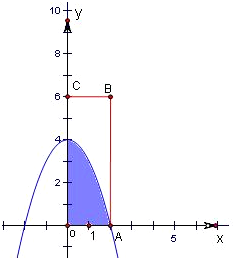 解:本题是一个几何概型,
解:本题是一个几何概型,
∵试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},
∴SΩ=2×6=12,
∵满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},即A={(x,y)|0≤x≤2,0≤y≤6,y≤4-x2},
∴SA=
(4-x2)dx=(4x-
x3)
=
,
∴由几何概型公式得到P=
=
.
故答案为:
.
 解:本题是一个几何概型,
解:本题是一个几何概型,∵试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},
∴SΩ=2×6=12,
∵满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},即A={(x,y)|0≤x≤2,0≤y≤6,y≤4-x2},
∴SA=
| ∫ | 2 0 |
| 1 |
| 3 |
| | | 2 0 |
| 16 |
| 3 |
∴由几何概型公式得到P=
| ||
| 2×6 |
| 4 |
| 9 |
故答案为:
| 4 |
| 9 |
点评:本题以二元一次不等式组表示的平面区域为例,求几何概型的概率,着重考查了简单线性规划和几何概型的概率求法等知识,属于中档题.

练习册系列答案
相关题目
若tan280°=a,则sin80°的结果为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、-
|
为了解本市的交通状况,某校高一年级的同学分成了甲、乙、丙三个组,从下午13点到18点,分别对三个路口的机动车通行情况进行了实际调查,并绘制了频率分布直方图(如图),记甲、乙、丙三个组所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为( )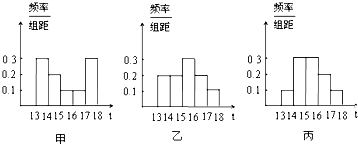

| A、s1>s2>s3 |
| B、s1>s3>s2 |
| C、s2>s3>s1 |
| D、s3>s2>s1 |
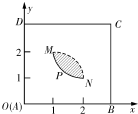 如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=
如图,矩形ABCD是一个观光区的平面示意图,建立平面直角坐标系,使顶点A在坐标原点O,B,D分别在x轴,y轴上,AD=3百米,AB=a百米(3≤a≤4)观光区中间叶形阴影部分MN是一个人工湖,它的左下方边缘曲线是函数y=