题目内容
空间四边形ABCD的每条边和对角线的长都等于a，点M、N分别是边AB、CD的中点，求证：（1）MN为AB和CD的公垂线；
（2）求MN的长；
（3）求异面直线AN与CM所成角的余弦值．
考点：异面直线及其所成的角
专题：空间角
分析：（1）如图所示，连接DM，CM．利用等腰三角形的性质和线面垂直的判定定理及性质定理可证AB⊥MN，CD⊥MN．即MN为AB和CD的公垂线．
（2）由（1）可得：在Rt△ACM中，利用勾股定理可得CM=
，在Rt△CMN中，同理可得MN=
即可．
（3）由于
=
+
+
，利用数量积的性质即可得出．
（2）由（1）可得：在Rt△ACM中，利用勾股定理可得CM=
| AC2-AM2 |
| CM2-CN2 |
（3）由于
| CA |
| CM |
| MN |
| NA |
解答：
证明：（1）如图所示，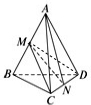
连接DM，CM．
∵空间四边形ABCD的每条边和对角线的长都等于a，点M、N分别是边AB、CD的中点，
∴CM⊥AB，DM⊥AB，CM∩DM=M，
∴AB⊥平面CMD，
∴AB⊥MN．
同理可证：CD⊥MN．
∴MN为AB和CD的公垂线．
（2）由（1）可得：在Rt△ACM中，CM=
=
=
a．
在Rt△CMN中，MN=
=
=
a．
（3）设异面直线AN与CM所成角为θ．
cos＜
，
＞=-
=-
=-
=cos＜
，
＞．
∵
=
+
+
，
∴
2=
2+
2+
2+2
•
+2
•
+2
•
，
∴a2=
+
+
+2×
a×
a•(-
)×2+2×
a×
a×cos＜
，
＞，
解得cos＜
，
＞=
，
∴cosθ=
．
连接DM，CM．∵空间四边形ABCD的每条边和对角线的长都等于a，点M、N分别是边AB、CD的中点，
∴CM⊥AB，DM⊥AB，CM∩DM=M，
∴AB⊥平面CMD，
∴AB⊥MN．
同理可证：CD⊥MN．
∴MN为AB和CD的公垂线．
（2）由（1）可得：在Rt△ACM中，CM=
| AC2-AM2 |
a2-(
|
| ||
| 2 |
在Rt△CMN中，MN=
| CM2-CN2 |
|
| ||
| 2 |
（3）设异面直线AN与CM所成角为θ．
cos＜
| CM |
| MN |
| MN |
| CM |
| ||||
|
| ||
|
| MN |
| NA |
∵
| CA |
| CM |
| MN |
| NA |
∴
| CA |
| CM |
| MN |
| NA |
| CM |
| MN |
| MN |
| NA |
| CM |
| NA |
∴a2=
| 3a2 |
| 4 |
| 2a2 |
| 4 |
| 3a2 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
|
| ||
| 2 |
| ||
| 2 |
| CM |
| NA |
解得cos＜
| CM |
| NA |
| 2 |
| 3 |
∴cosθ=
| 2 |
| 3 |
点评：本题考查了等腰三角形的性质、线面垂直的判定定理及性质定理、异面直线的公垂线、勾股定理、数量积的性质、异面直线所成的夹角等基础知识与基本技能方法，考查了推理能力和计算能力，考查了空间想象能力，属于难题．
练习册系列答案
名校课堂系列答案
相关题目
设△ABC的内角A、B、C的对边分别为a、b、c，若
=
=
，则△ABC是（ ）
| a | ||
cos
|
| b | ||
cos
|
| c | ||
cos
|
| A、直角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
如图所示，AT切⊙O于T，若AT=2
，AE=3，AD=4，DE=2，则BC等于（ ）
| 6 |
| A、3 | B、4 | C、6 | D、8 |
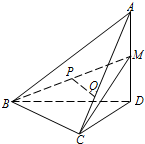如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2