题目内容
已知(1+mx)n(m∈R,n∈N*)的展开式的二项式系数之和为32,且展开式中含x3项的系数为80.
(1)求m,n的值;
(2)求(1+mx)n(1-x)6展开式中含x2项的系数.
(1)求m,n的值;
(2)求(1+mx)n(1-x)6展开式中含x2项的系数.
考点:二项式系数的性质,二项式定理的应用
专题:二项式定理
分析:(1)根据2n=32求得n的值.在通项Tr+1=
mrxr(r=0,1,…,5),令x的幂指数r=3,可得展开式中含x3项的系数为
m3=80,从而求得m的值.
(2)本题即求(1+2x)5(1-x)6展开式中含x2项的系数,利用通项公式展开化简可得展开式中含x2项的系数.
| C | r 5 |
| C | 3 5 |
(2)本题即求(1+2x)5(1-x)6展开式中含x2项的系数,利用通项公式展开化简可得展开式中含x2项的系数.
解答:
解:(1)由题意,2n=32,则n=5.
由通项Tr+1=
mrxr(r=0,1,…,5),
令r=3,可得展开式中含x3项的系数为
m3=80,所以m=2.
(2)即求(1+2x)5(1-x)6展开式中含x2项的系数,
(1+2x)5(1-x)6=[
+
(2x)1+
(2x)2+…](
-
x+
x2+…)
=(1+10x+40x2+…)(1-6x+15x2+…),
所以展开式中含x2项的系数为1×15+10×(-6)+40×1=-5.
由通项Tr+1=
| C | r 5 |
令r=3,可得展开式中含x3项的系数为
| C | 3 5 |
(2)即求(1+2x)5(1-x)6展开式中含x2项的系数,
(1+2x)5(1-x)6=[
| C | 0 5 |
| C | 1 5 |
| C | 2 5 |
| C | 0 6 |
| C | 1 6 |
| C | 2 6 |
=(1+10x+40x2+…)(1-6x+15x2+…),
所以展开式中含x2项的系数为1×15+10×(-6)+40×1=-5.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于非零向量
、
,下列命题中正确的是( )
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),那么数列{an}的前50项和S50的最小值为( )
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
等差数列{an}中,a3+a7=15,则a2+a8=( )
| A、10 | B、15 | C、12 | D、8 |
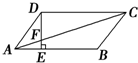 如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )
如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )| A、54cm2 |
| B、24cm2 |
| C、18cm2 |
| D、12cm2 |
 空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证:
空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证: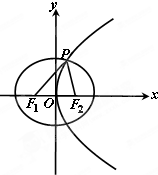 已知离心率为
已知离心率为 如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设
如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设