题目内容

设△ABC的内角A、B、C的对边分别为a、b、c，若
a
cos
A
2
=
b
cos
B
2
=
c
cos
C
2
，则△ABC是（　　）
A、直角三角形
B、钝角三角形
C、等腰直角三角形
D、等边三角形
考点：正弦定理
专题：解三角形
分析：由条件利用正弦定理、二倍角的正弦公式求得sin
A
2
=sin
B
2
=sin
C
2
，可得A=B=C，三角形为等边三角形．
解答： 解：△ABC中，∵
a
cos
A
2
=
b
cos
B
2
=
c
cos
C
2
，
∴利用正弦定理可得
sinA
cos
A
2
=
sinB
cos
B
2
=
sinC
cos
C
2
，
化简可得sin
A
2
=sin
B
2
=sin
C
2
，
∴A=B=C，故三角形为等边三角形，
故选：D．
点评：本题主要考查正弦定理的应用，二倍角的正弦公式，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=2cos2
x
2
+sinx．
（1）求f（x）的最小正周期和单调递增区间；
（2）求f（x）在区间[0，π]上的最大值与最小值．
复平面内，复数z=
2+i
i2013
，则复数z的共轭复数
.
z
对应的点的象限是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
给出下列命题：
①终边相同的角的同名函数值相等；
②终边不同的角的同名函数值不相等；
③若sinα＞0，则α是第一或第二象限的角；
④若α是第二象限角，且P（x，y）是其终边上的一点，则cosα=
-x
x2+y2
；
⑤若α、β是第二象限的角，且α＞β，则cosα＜cosβ．
其中正确的命题有（　　）
A、1个B、2个C、3个D、4个
对于非零向量
a
、
b
，下列命题中正确的是（　　）
A、
a
∥
b
⇒
a
在
b
上的投影为|
a
|
B、
a
•
b
=0⇒
a
=0或
b
=0
C、
a
⊥
b
⇒
a
•
b
=（
a
•
b
）2
D、
a
•
c
=
b
•
c
⇒
a
=
b
若a=21.2，b=(
1
2
)-0.8，c=2log52，则（　　）
A、c＜b＜a
B、b＜a＜c
C、c＜a＜b
D、b＜c＜a
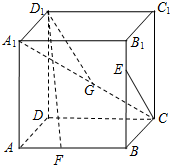已知正方体ABCD-A1B1C1D1，点E，F，G分别是线段B1B，AB和A1C上的动点，观察直线CE与D1F，CE与D1G．给出下列结论：
①对于任意给定的点E，存在点F，使得D1F⊥CE；
②对于任意给定的点F，存在点E，使得CE⊥D1F；
③对于任意给定的点E，存在点G，使得D1G⊥CE；
④对于任意给定的点G，存在点E，使得CE⊥D1G．
其中正确结论的序号是（　　）
A、①③B、①④C、②③D、②④
下列命题正确的个数是（　　）
（1）若直线l上有无数个点不在α内，则l∥α
（2）若直线l与平面α平行，l与平面α内的任意一直线平行
（3）两条平行线中的一条直线与平面平行，那么另一条也与这个平面平行
（4）若一直线a和平面α内一直线b平行，则a∥α
A、0个B、1个C、2个D、3个
空间四边形ABCD的每条边和对角线的长都等于a，点M、N分别是边AB、CD的中点，求证：
（1）MN为AB和CD的公垂线；     
（2）求MN的长；
（3）求异面直线AN与CM所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网