题目内容
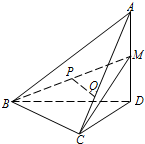 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2| 2 |
(1)证明:PQ∥平面BCD;
(2)若∠BDC=45°,求直线BM与平面ABC所成角的余弦值.
考点:直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)取BD的中点O,在线段CD上取点F,使得DF=3FC,连接OP,OF,FQ.先证明出四边形OPQF是平行四边形,进而证明出PQ∥OF,最后根据线面平行的判定定理证明出PQ∥平面BCD.
(2)先证明∠MBK为所求角,分别求得BM,MK,求得cos∠MBK的值.
(2)先证明∠MBK为所求角,分别求得BM,MK,求得cos∠MBK的值.
解答:
(1)证明:取BD的中点O,在线段CD上取点F,使得DF=3FC,连接OP,OF,FQ.
∵AQ=3QC,
∴QF∥AD,且QF=
AD,
∵O,P分别为BD,BM的中点,所以OP是△BDM的中位线,
∴OP∥DM,且OP=
DM,
又点M是AD的中点,
∴OP∥AD,且OP=
AD
∴OP∥FQ,且OP=FQ
∴四边形OPQF是平行四边形,
∴PQ∥OF,
又∵PQ?平面BCD,OF?平面BCD,
∴PQ∥平面BCD.
(2)解:过M做MK⊥AC,交AC于点K,连结BK,
∵BC⊥CD,BC⊥AD,CD∩AD=D,
∴BC⊥平面ADC,
又∵BC?平面ABC,
∴平面ACD⊥平面ABC,
∵平面ACD∩平面ABC=AC,MK⊥AC,
∴MK⊥平面ABC,
∴∠MBK就是所求,
在Rt△BDM中,BD=2
,MD=1
∴BM=3,
∵在Rt△AMC中,AM=1,AC=2
,且AC•MK=AM•CD,
∴MK=
,
∴在Rt△MKB中,cos∠MBK=
=
=
.

∵AQ=3QC,
∴QF∥AD,且QF=
| 1 |
| 4 |
∵O,P分别为BD,BM的中点,所以OP是△BDM的中位线,
∴OP∥DM,且OP=
| 1 |
| 2 |
又点M是AD的中点,
∴OP∥AD,且OP=
| 1 |
| 4 |
∴OP∥FQ,且OP=FQ
∴四边形OPQF是平行四边形,
∴PQ∥OF,
又∵PQ?平面BCD,OF?平面BCD,
∴PQ∥平面BCD.
(2)解:过M做MK⊥AC,交AC于点K,连结BK,
∵BC⊥CD,BC⊥AD,CD∩AD=D,
∴BC⊥平面ADC,
又∵BC?平面ABC,
∴平面ACD⊥平面ABC,
∵平面ACD∩平面ABC=AC,MK⊥AC,
∴MK⊥平面ABC,
∴∠MBK就是所求,
在Rt△BDM中,BD=2
| 2 |
∴BM=3,
∵在Rt△AMC中,AM=1,AC=2
| 2 |
∴MK=
| ||
| 2 |
∴在Rt△MKB中,cos∠MBK=
| BK |
| BM |
| ||
| BM |
| ||
| 6 |

点评:本题主要考查了线面平行的判定,直线与平面所成的角.考查了学生综合运用基础知识解决问题的能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证:
空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证: 如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设
如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设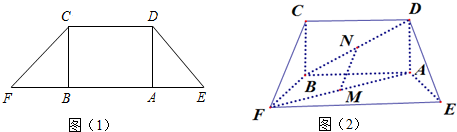


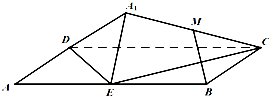 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是