题目内容
如图所示,AT切⊙O于T,若AT=2
,AE=3,AD=4,DE=2,则BC等于( )

| 6 |

| A、3 | B、4 | C、6 | D、8 |
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:利用AT为⊙O的切线,求出AT,证明△EAD∽△CAB,可得
=
,即可求出BC.
| DE |
| BC |
| AE |
| AC |
解答:
解:∵AT为⊙O的切线,∴AT2=AD•AC.
∵AT=2
,AD=4,∴AC=6.
∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB,即
=
,
∴BC=
=
=4.
故选:B.
∵AT=2
| 6 |
∵∠ADE=∠B,∠EAD=∠CAB,
∴△EAD∽△CAB,即
| DE |
| BC |
| AE |
| AC |
∴BC=
| DE•AC |
| AE |
| 2×6 |
| 3 |
故选:B.
点评:本题考查切割线定理,考查三角形相似的判断与性质,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复平面内,复数z=
,则复数z的共轭复数
对应的点的象限是( )
| 2+i |
| i2013 |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列命题正确的个数是( )
(1)若直线l上有无数个点不在α内,则l∥α
(2)若直线l与平面α平行,l与平面α内的任意一直线平行
(3)两条平行线中的一条直线与平面平行,那么另一条也与这个平面平行
(4)若一直线a和平面α内一直线b平行,则a∥α
(1)若直线l上有无数个点不在α内,则l∥α
(2)若直线l与平面α平行,l与平面α内的任意一直线平行
(3)两条平行线中的一条直线与平面平行,那么另一条也与这个平面平行
(4)若一直线a和平面α内一直线b平行,则a∥α
| A、0个 | B、1个 | C、2个 | D、3个 |
已知各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),那么数列{an}的前50项和S50的最小值为( )
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
阅读如图程序:如果输入5,则该程序运行结果为( )


| A、1 | B、10 | C、25 | D、26 |
等差数列{an}中,a3+a7=15,则a2+a8=( )
| A、10 | B、15 | C、12 | D、8 |
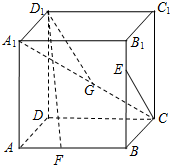 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: 空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证:
空间四边形ABCD的每条边和对角线的长都等于a,点M、N分别是边AB、CD的中点,求证: